PHYS 1120 Work & Energy Solutions

Questions:

Physics 1120: Work & Energy Solutions

Energy

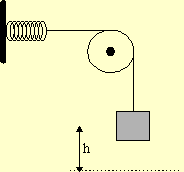
In the diagram below, the spring has a force constant of 5000 N/m, the block has a mass of 6.20 kg, and the height h of the hill is 5.25 m. Determine the compression of the spring such that the block just makes it to the top of the hill. Assume that there are no non-conservative forces involved.

Since the problem involves a change is height and has a spring, we make use of the Generalized Work-Energy Theorem. Since the initial and final speeds are zero,

W_NC = ΔE = U_grav
f - U_spring _i = mgh - ½Kx² .

There are no nonconservative forces so W_NC = 0. Getting x by itself yields

x = [2mgh / K]^½ = 0.357 m .

A solid ball, a cylinder, and a hollow ball all have the same mass m and radius R. They are allowed to roll down a hill of height H without slipping. How fast will each be moving on the level ground?

The only external force on the object, excluding gravity which is taken into account through gravitational potential energy, is static friction. For objects which roll across a stationary surface, static friction does no work, so here 0 = ΔE, where E is the observable or mechanical energy.

As the object drops down the hill, it loses gravitational potential energy while it gains both linear and rotational kinetic energy. Thus we have

0 = -mgH + ½mv² + ½Iω²

Now since the object rolls without slipping, the angular velocity ω is related to the linear velocity v by ω = v/R. So our equation becomes

0 = -mgH + ½mv² + ½I(v/R)²

Isolating v² terms, we find v²[m + I/R²] = 2mgH. Solving for v we get

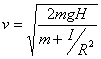
To proceed further, we need to know the moment of inertia of each object about its CM. We consult a table of moments of inertia and find

Shape	I_CM	v
solid sphere	²/₅MR²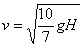
solid cylinder	½MR²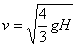
hollow sphere	²/₃MR²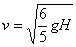

A cylinder of mass M and radius R, on an incline of angle θ, is attached to a spring of constant K. The spring is not stretched. Find the speed of the cylinder when it has rolled a distance L down the incline.

The only external force on the system, excluding gravity which is taken into account through gravitational potential energy, is static friction. For objects which roll across a stationary surface, static friction does no work, so here 0 = ΔE, where E is the observable or mechanical energy.

As the object rolls distance L down the incline, it loses gravitational potential energy while it gains both linear and rotational kinetic energy. Moreover, the spring gains Spring Potential Energy. Thus we have

0 = -mgH + ½mv² + ½Iω² + ½KL²

The relationship between H and the L is H = Lsinθ. Since the object rolls without slipping, the angular velocity ω is related to the linear velocity v by ω = v/R. Furthermore, consulting a table of values, the moment of inertia of a cylinder about the perpendicular axis through the CM, is ½MR². Our equation becomes

0 = -mgLsinθ + ½mv² + ½(½MR²)(v/R)² + ½KL²

Isolating v² terms, we find v²[½m + ¼m] = mgLsinθ - ½KL². Solving for v we get

A block of mass m is connected by a string of negligible mass to a spring with spring constant K which is in turn fixed to a wall. The spring is horizontal and the string is hung over a pulley such that the mass hangs vertically. The pulley is a solid disk of mass M and radius R. As shown in the diagram below, the spring is initially in its equilibrium position and the system is not moving.
(a) Use energy methods, to determine the speed v of the block after it has fallen a distance h. Express your answer in terms of g, m, K, M, and h.
(b) The block will oscillate between its initial height and its lowest point. At its lowest point, it turns around. Use your answer to part (a) to find where it turns around.
(c) Use your answer to part (a) and calculus to find the height at which the speed is a maximum.

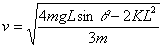
(a) The problem involves a change in height and speed and has a spring, so we would apply the generalized Work-Energy Theorem even if not directed to do,

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) , (1)

where K is the sum of all the linear and rotational kinetic energies of each object, and U is the sum of the spring and gravitational potential energies. Since there is no kinetic friction acting on the system, W_NC = 0.

Examining the problem object by object we see that the spring stretches, so there is an increase in spring potential energy. The pulley starts rotating, so there is an increase in its rotational kinetic energy. The block drops, so there is a decrease in its gravitational potential energy. As well, as the block drop, it increases its kinetic energy. Equation (1) for this problem is thus

0 = ½Kx² + ½Iω ² - mgh + ½mv² .

Since the spring is connected to the block, the spring stretches as much as the block drops, so x = h. We are told that the pulley is a solid disk, so I = ½MR². Since the rope does not slip the tangential speed of the pulley is the same as the rope and thus ω = v/R. Substituting these relations back into our equation yields,

0 = ½Kh² + ¼Mv² - mgh + ½mv² .

Collecting the terms with v, and solving for v yields

v = [(2mgh - kh²) / (m + M/2)]^½. (2)

(b) Recall from our discussions on kinematics that an object turns around when its velocity is zero. Setting equation (2) to zero

[(2mgh - kh²) / (m + M/2)]^½ = 0 ,

we see that the numerator is zero when

2mgh - kh²= 0 .

Solving this for h reveals that the object turns around when h = 2mg/k.

dv/dh = ½{1/[(2mgh - kh²) / (m + M/2)] ^½}[2mg-2kh]/[m+M/2] = 0 .

We see that the numerator to zero when

2mg-2kh = 0 .

Solving this for h reveals that the object turns around when h = mg/k, halfway between the starting position and the turnaround point.

A system of weights and pulleys is assembled as shown below. The pulleys are all fixed. The pulleys on the sides are disks of mass m_d and radius R_d; the central pulley is a hoop of mass m_h and radius R_h. A massless ideal rope passes around the pulleys and joins two weights. The rope does not slip. The two weights have masses m₁ and m₂ respectively. Use energy methods to find the velocity of the weights as a function of displacement, x. The moment of inertia of a disk is I_disk = ½MR² and of a hoop is I_hoop = MR².
The problem involves changes in height, speed, and rotation, so we would apply the generalized Work-Energy Theorem even if not directed to do,

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) , (1)
where K is the sum of all the linear and rotational kinetic energies of each object, and U is the sum of the gravitational potential energies. Since there is no kinetic friction acting on the system, W_NC = 0.

Let's assume block 2 moves down. Thus block 1 moves up an identical amount h. Since block 2 drops, there is a decrease in its gravitational potential energy. Block 1 will increase its potential energy. As well, as both blocks move, they increases its kinetic energy. The pulleys start rotating, so there is an increase in the rotational kinetic energy of each. Equation (1) for this problem is thus

0 = -m₂gh + m₁gh + ½m₂v² + ½m₁v² + 2×½I_D (ω_D)² + ½I_H(ω_H) ² .

We are told that I_disk = ½M_D(R_D)² and I_hoop = M_H(R_H)². Since the rope does not slip the tangential speed of the pulleys is the same as the rope and thus ω = v/R. Substituting this relations back into our equation yields,

0 = -(m₂- m₁)gh + ½m₂v² + ½m₁v² + ½M_D(R_D)²(v/R_D)² + ½ M_H(R_H)²(v/R_H)² .

Collecting the terms with v, and solving for v yields
v = [2(m₂ - m₁)gh / (m₁ + m₂ + M_D+ M_H)]^½.
In the diagram below, a moving skier on top of a circular hill of radius R_h = 62.0 m feels that his "weight" is only (3/8)mg. What would be the skier's apparent weight (in multiples of mg) at the bottom of the circular valley which has a radius R_v= 43.0 m? Neglect friction and air resistance.

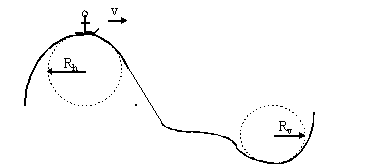
The problem involves a change in height and speed, so we apply the generalized Work-Energy Theorem.

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) = [½m(v_v)² -2mgR_v] - [½m(v_h)² + 2mgR_h] .

There is no friction or air resistance, W_NC = 0. Our equation is thus

0 = [½m(v_v)² - 2mgR_v] - [½m(v_h)² + 2mgR_h] . (1)

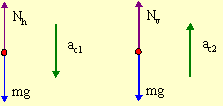
We told what the skier feels his weight to be. The sensation of weight is N, the normal acting on the person. To find a force we need to draw a FBD and apply Newton's Second Law. We must do this both at the top of the hill and at the bottom of the valley. Since both are circular paths, we are dealing with centripetal acceleration.

	hill	valley
	ΣF_y = ma_y	ΣF_y = ma_y
	N_h - mg = -m(v_h)²/R_h	N_v - mg = m(v_v)²/R_v

We are told that N_h = (3/8)mg, so the first force equation becomes (5/8)mg = m(v_h)²/R_h. Solving for v_h, we find v_h = [(5/8)gR_h]^½. This can be substituted into equation (1)

0 = [½(v_v)² - 2gR_v] - [½{(5/8)gR_h} + 2gR_h] .

Rearranging to isolate v_v, we find

v_v = [g{(37/8)R_h + R_v}] ^½ = 67.08 m/s .

This result, along with the second force equation let's find the apparent weight in the valley,

N_v = mg + m(v_v)²/R_v = mg[1+{(37/8)R_h+R_v}/R_v] = mg[2+(37/8)( R_h/R_v)] =(11.7)mg .

The skier feels 11.7 times heavier at bottom of valley - which is not very likely!

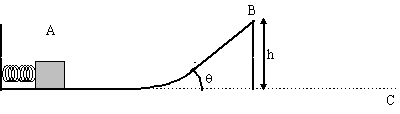
At point A in the figure shown below, a spring (spring constant k = 1000 N/m) is compressed 50.0 cm by a 2.00 kg block. When released the block travels over the frictionless track until it is launched into the air at point B. It lands at point C. The inclined part of the track makes an angle of θ = 55.0° with the horizontal and point B is a height h = 4.50 m above the ground. How far horizontally is point C from point B?

The problem involves a change in height and speed and has a spring, so we apply the generalized Work-Energy Theorem., W_NC = ΔE.

There is no friction or air resistance, so W_NC = 0. The spring is compressed initially, so it loses spring potential energy. The block increases kinetic energy and gains gravitational potential energy. Our equation is thus

0 = -½kx² + ½mv² + mgh .

We can use this to find the speed of the block at launch

v = [kx²/m - 2gh]^½ = [(1000)(0.5)²/2 - 2(9.81)(4.5)]^½ = 6.0589 m/s .

Now the block is a projectile. To solve a projectile problem we break the motion into its x and y components and apply our kinematics equations.

i	j
v_0x = vcos(55º) = 3.47523 m/s	v_0y = vsin(55º) = 4.96314 m/s
Δx = ?	Δy = -4.50 m
a_x = 0	a_y = -9.81 m/s²
t = ?	t = ?

We have enough information in the y column to find t using Δy = v_0yt + ½at² ,

-4.50 = 4.96314t - 4.905t² .

Using the quadratic equation, the solutions are t = -0.5773 s and t = 1.5892 s. We want the positive, or forward in time, solution. Hence the horizontal distance traveled by the block is

Δx = v_0xt = 3.47523 × 1.5892 = 5.52 m .

Point C is therefore 5.52 m from B.

A small solid sphere of radius r = 1.00 cm and mass m = 0.100 kg at point A is pressed against a spring and is released from rest with the spring compressed 20.0 cm from its natural length. The spring has a force constant k = 20.0 N/m. The sphere rolls without slipping along a horizontal surface to point B where it smoothly continues onto a circular track of radius R = 2.00 m. The ball finally leaves the surface of the track at point C. Find the angle θ where the ball leaves the track. Assume that friction does no work. Hint - find an expression for the speed of the sphere at point C. The moment of inertia of a sphere is I = ²/₅mr².

The problem involves a change in height and speed and has a spring, so we apply the generalized Work-Energy Theorem., W_NC = ΔE.

We are told to assume W_NC = 0. The spring is compressed initially, so it loses spring potential energy. The ball increases both linear and rotational kinetic energy. The ball loses gravitational potential energy. Our equation is thus

0 = -½kx² + ½mv² + ½Iω² - mgh . (1)
We are told the moment of inertia, I, and we are told that the ball does not slip so ω = v/r. Using some trigonometry, the distance dropped is h = (R+r) - (R+r)cosθ. Using these results with equation (1) yields

0 = -½kx² + (7/10)mv² - mg(R+r)[1 - cosθ] . (2)
We have two unknowns, v and θ. To proceed further we note that the ball loses contact with the surface. Recall that losing contact implies that N = 0. The normal is a force and to find forces we draw a FBD and apply Newton's Second Law. Since the ball moves in a circle, we are dealing with centripetal acceleration.

j

ΣF_y = ma_y

N - mgcosθ = -mv²/(R+r)

Since N = 0, and after some rearranging, the force equation yields
v² = (R+r)gcosθ .

Substituting this into equation(2), we get
0 = -½kx² + (7/10)mg(R+r)cosθ - mg(R+r)[1 - cosθ] .

Collecting terms with cos on the left-hand side yields

(17/10)mg(R+r)cosθ = ½kx² + mg(R+r) .

Solving for θ,

θ = cos^-1 {[½kx² + mg(R+r)] / (17/10)mg(R+r)} = 44.9º .
The ball comes off the surface when the angle is 44.9º.
The potential energy of a system of particles in one dimension is given by:

,
where the potential energy is in Joules. What is the work done in moving a particle in this potential from x = 1 m to x = 2 m? What is the force on a particle in this potential at x = 1 m and at x = 2 m? Where are the points of stable and unstable equilibrium (peaks and troughs)?

Assuming the particle starts and ends at rest, the work done is

W_NC = U_f - U_i = [5-2+3(2)²-2(2)³] - [5-1+3(1)²-2(1)³] = -2 J - 5 J = -7 J .

Force is the negative derivative of the potential,

F = -dU/dx = 1 - 6x - 6x² .

Thus the force at x = 1 m is

F = 1 - 6(1) -6(1)² = 1 N ,

and at x = 2 m is

F = 1 - 6(2) -6(2)² = 13 N .

The equilibrium points occur at the minima and maxima of U(x). We find them by setting dU/dx = 0, or

-1 + 6x - 6x² = 0.

This equation has roots at x = 0.211 m and x = 0.789 m.

Looking at the second derivative,

d²U/d²x = 6 - 12x .

We see that when x = 0.211 m, d²U/d²x = 6 - 12(0.211) > 0, so x = 0.211 m is a minimum. We also see that when x = 0.789 m, d²U/d²x = 6 - 12(0.789) < 0, so x = 0.789 m is a maximum.
The PE curve for a 2.5-kg particle under the influence of a conservative force is shown below. (a) What would be the total mechanical energy of the system, if one know that the particle has a speed of 7.5 m/s at x = 1.5 m? (b) If E_tot = 150 J, where would the particle have zero velocity? Where would the particle have its maximum kinetic energy and what would be its speed there? (c) What is the minimum total energy for which the particle escapes the influence of the force creating the potential (i.e. the particle escapes the potential well)?

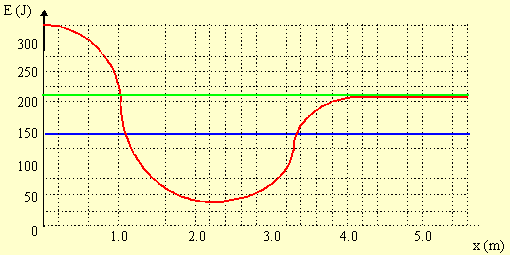
(a) The kinetic energy of the particle is
K = ½mv² = ½(2.5 kg)(7.5 m/s)² = 70.3 J.

Examining the graph, at x = 1.5 m, the potential energy approximately U = 75 J. So the total energy is E_total= K + U = 145 J.

(b) Zero velocity implies zero kinetic energy. Thus all the energy would have to be potential. Examining the graph, we see that E_total = 150 J intercepts the potential energy curve at x = 1.1 m and at x = 3.4 m.

The maximum kinetic energy would occur where the potential energy is a minimum. Examining the graph the minimum potential is at x = 2.2 m, and is 40 J. The kinetic energy is K = E_total - U = 150 J - 40 J = 110 J.

Since K = ½mv²
v = [2K/m]^½ = [2(110 J)/2.5 kg)]^½ = 9.4 m/s .

(c) Examining the graph, a particle with an energy of about 210 J could escape the potential well.

Work and Energy

In the diagram below, calculate the work done if:
(a) F = 15.0 N, θ = 15°, and Δx = 2.50 m,
(b) F = 25.0 N, θ = 75°, and Δx = 12.0 m,
(c) F = 10.0 N, θ = 135°, and Δx = 5.50 m,

For constant forces, work is defined by W = FΔxcos(θ).
(a) W = 36.2 J
(b) W = 77.6 J
(c) W = -38.9 J

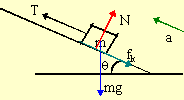
In the diagram below, a rope with tension T = 150 N pulls a 15.0-kg block 3.0 m up an incline (θ = 25.0°). The coefficient of kinetic friction is μ_k= 0.20. Find the work done by each force acting on the block.

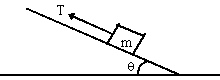
To find the work done by a force, we need to know the magnitude of the force and the angle it makes with the displacement. To find forces, we draw a FBD and use Newton's Second Law.

i j

ΣF_x = ma_x ΣF_y = ma_y

T - f_k - mgsinθ = ma N - mgcosθ = 0

The second equation informs us that N = mgcosθ. We know f_k = μ_kN = μ_kmgcosθ.

Force Force (N) φ W = FΔxcosφ (J)

Tension 150 0 450

Weight 147.15 θ + π/2 -187

Normal 133.36 π/2 0

Friction 26.67 π -80

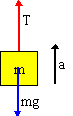
A winch lifts a 150 kg crate 3.0 m upwards with an acceleration of 0.50 m/s². How much work is done by the winch? How much work is done by gravity?

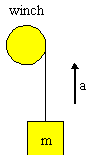
To find the work done by a force, we need to know the magnitude of the force and the angle it makes with the displacement. To find forces, we draw a FBD and use Newton's Second Law.

j

ΣF_y = ma_y

T - mg = ma

The work done by the winch is the work done by tension. The work done by gravity is the work done by the objects weight. Since we know m and g, we find T = mg + ma = 1546.5 N. The work done by tension is W_tension = TΔycos(0) = 4.64 × 10³ J. The work done by gravity is W_gravity = mgΔy cos(π) = -4.41 × 10³ J.
What work does a baseball bat do on a baseball of mass 0.325 kg which has a forward sped of 36 m/s and a final speed of 27 m/s backwards. Assume motion is horizontal.

Since we are asked for the work done and have a change in speed, we make use of the generalized Work-Energy Theorem. Since the height of the ball does not change, there is only a change in kinetic energy.

W_NC = ΔE = K_f - K_i = ½m[(v_f)² - (v₀)²] = ½(0.325kg)[(-27 m/s)² - (36 m/s)²] = -92.1 J .

What is the work done by friction in slowing a 10.5-kg block traveling at 5.85 m/s to a complete stop in a distance of 9.65 m? What is the kinetic coefficient of friction?

Since we are asked for the work done and have a change in speed, we make use of the generalized Work-Energy Theorem. Since the height of the block does not change, there is only a change in kinetic energy.

W_friction = ΔE = K_f - K_i = ½m[(v_f)² - (v₀)²] = ½(10.5kg)[(0)² - (5.85 m/s)²] = 179.67 J .

To find μ, we need to know the force and the angle it makes with the displacement. To find forces, we draw a FBD and use Newton's Second Law.

	i	j
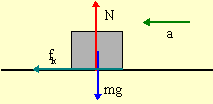	ΣF_x = ma_x	ΣF_y = ma_y
	-f_k = -ma	N - mg = 0

The second equation gives N = mg and we know f_k = μ_k N, so f_k = μ_k mg. Therefore, the work done by friction is W_friction = -f_kΔx = -μ_kmgΔx. Rearranging this yields

μ_k = -W_friction / mgΔx = 0.18 .

A 50.0-N force is applied horizontally to a 12.0-kg block which is initially at rest. After traveling 6.45 m, the speed of the block is 5.90 m/s. What is the coefficient of kinetic friction?

Since the problem involves a change is speed, we make use of the Generalized Work-Energy Theorem

W_NC = ΔE = K_f - K_i = ½m[(v_f)² - (v₀)²] = ½m(v_f)² .

There are two nonconservative forces in this problem, friction and the applied force. The work done by friction is given by W_friction = -f_kΔx. The work done by the applied force is W_F = FΔx.

FΔx - f_kΔx = ½m(v_f)² . (1)

To find out more about f_k, we draw a FBD and use Newton's Second Law.

	i	j
	ΣF_x = ma_x	ΣF_y = ma_y
	F - f_k = ma	N - mg = 0

The second equation gives N = mg and we know f_k = μ_kN, so f_k = μ_kmg. Thus W_friction = -μ_kmgΔx. Combining this result with equation (1), we get

(F - μ_kmg)Δx = ½m(v_f)² .

Rearranging yields an expression for μ_k

μ_k = [FΔx - ½m(v_f)²] / mgΔx .

Using the given values, we find μ_k = 0.15 .

A rope is wrapped abound a cylindrical drum as shown below. It is pulled with a constant tension of 100 N for six revolutions of the drum. The drum has a radius of 0.500 m. A brake is also applying a force to the drum. The brake pushes inwards on the drum with a force of 200 N. The pressure point is 0.350 m from the centre of the drum. The coefficient of kinetic friction between the brake and the drum is 0.50. Determine the work done by each torque.

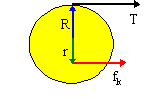Work is defined by the formula W = τΔφ in rotational cases. Since the rope does not slip as it is pulled, the object rotates 6 times clockwise or Δφ = -12π. We know f_k = μ_kN. In this problem, N equals how hard the brake is pressed. Note that the tension and the friction are tangential to the drum.

(a) W_T = (-RT)Δφ = -(0.5m)(100 N)(-12π) = 1.88 × 10³ J.

(b) W_f = (rf_k)Δφ = (0.35 m)(0.50 × 200 N)(-12π) = -1.32 × 10³ J.
Determine the work done by the following. Determine the angles between the forces and the displacements. The forces are in Newtons and the displacements are in metres:

(a) F = (1, 2, 3) and Δr = (4, 5, 6)
(b) F = (1, 2, 3) and Δr = (4, 5, -6)
(c) F = (4, 2, 4) and Δr = (2, -8, 2)

In 3D, work is defined W = F · Δr, which means W = F_xΔx + F_yΔy + F_zΔz. It is also defined by W = FΔrcosθ, where F and R are the magnitudes of the vectors, F and Δr. Using the 3D version of Pythagoras' Theorem, F = [(F_x)² + (F_y)² + (F_z)²]^½ and Δr = [(Δx)² + (Δy)² + (Δz)²]^½. If we find the work using the first form, then θ can be found from the second by θ = cos^-1(W / FΔr).

(a) W = 1×4 + 2×5 + 3×6 = 32 J.

Since F = [(1)²+ (2)² + (3)²]^½ = 3.7417 N and Δr = [(4)² + (5)² + (6)²]^½ = 8.7750 m, then θ = cos^-1(W / FΔr) = 12.9º.

(b) W = 1×4 + 2×5 + 3×(-6) = -4 J.

Since F = [(1)² + (2)² + (3)²]^½ = 3.7417 N and Δr = [(4)² + (5)² + (-6)²]^½ = 8.7750 m, then θ = cos^-1(W / FΔr) = 97.0º.

(c) W = 4×2 + 2×(-8) + 4×2 = 0 J.

Since F = [(4)²+ (2)² + (4)²]^½ = 6.1644 N and Δr = [(2)² + (-8)² + (2)²]^½ = 8.4853 m, then θ = cos^-1(W / FΔr) = 90º.

In the diagram below, a 5.00-kg block slides from rest at a height of h₁ = 1.75 m down to a horizontal surface where it passes over a 2.00 m rough patch. The rough patch has a coefficient of kinetic friction μ_k = 0.25. What height, h₂, does the block reach on the θ = 30.0° incline?

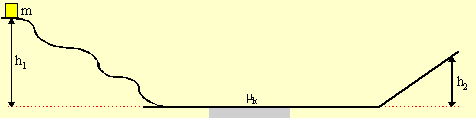
Since the problem involves a change of height and speed, we make use of the Generalized Work-Energy Theorem. Since the block's initial and final speeds are zero, we have

W_NC = ΔE = U_f - U_i = mgh₂ - mgh₁ . (1)

The nonconservative force in this problem is friction. To find the work done by friction, we need to know the friction. To find friction, a force, we draw a FBD at the rough surface and use Newton's Second Law.

	i	j
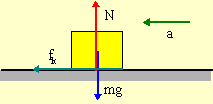	ΣF_x = ma_x	ΣF_y = ma_y
	-f_k = -ma	N - mg = 0

The second equation gives N = mg and we know f_k = μ_kN, so f_k = μ_kmg. Therefore, the work done by friction is W_friction = -f_kΔx = -μ_kmgΔx. Putting this into equation (1) yields

-μ_kmgΔx = mgh₂ - mgh₁ .

Solving for h₂, we find

h₂ = h₁ - μ_kΔx = 1.25 m .

In the diagram below, a 5.00-kg block slides from rest at a height of h₁ = 1.75 m down to a smooth horizontal surface until it encounters a rough incline. The incline has a coefficient of kinetic friction μ_k = 0.25. What height, h₂, does the block reach on the θ = 30.0° incline?

Since the problem involves a change of height and speed, we make use of the Generalized Work-Energy Theorem. Since the block's initial and final speeds are zero, we have

W_NC = ΔE = U_f - U_i = mgh₂ - mgh₁ . (1)

	i	j
	ΣF_x = ma_x	ΣF_y = ma_y
	-f_k - mgsinθ = -ma	N - mgcosθ = 0

The second equation gives N = mgcosθ and we know f_k = μ_kN, so f_k = μ_k mgcosθ. Therefore, the work done by friction is W_friction = -f_kΔx = -μ_kmg cosθΔx. Putting this into equation (1) yields

-μ_kmgcosθΔx = mgh₂ - mgh₁ .

A little trigonometry shows that Δx is related to h₂ by Δx = h₂ / sinθ. Putting this into the above equation yields

-μ_kcosθ [h₂ / sinθ] = h₂ - h₁ .

Solving for h₂, we find

h₂ = h₁ / [1 + μ_k/tanθ] = 1.22 m .

A rope is wrapped exactly three times around a cylinder with a fixed axis of rotation at its centre. The cylinder has a mass of 250 kg and a diameter of 34.0 cm. The rope is pulled with a constant tension of 12.6 N. The moment of inertia of a cylinder about its centre is I = ½MR². (a) What is the work down by the rope as it is pulled off the cylinder. Note that the rope does not slip. (b) If the cylinder was initially at rest, what is its final angular velocity? Note that ropes are always tangential to the surfaces that they are wrapped around. Note that the work done by the tension is non-conservative.

Since the problem involves a change is speed, we make use of the Generalized Work-Energy Theorem. Since there is only a change in rotational speed,

W_NC = ΔE = K_f - K_i = ½I[(ω_f)² - (ω₀)²] = ½I(ω_f)² .
The nonconservative force in this problem is tension, W_NC = W_T. So we have

W_T = ½I(ω_f)² . (1)
(a) The definition of work in rotational situations is W = τΔφ. Tension is always tangential to cylinders so τ_T = -RT. Since the rope does not slip, the cylinder rotates clockwise three times so Δφ = -6π. We can thus find the work done by the tension
W_T = (-RT)(-6π) = (0.34 m)(12.6 N)6π = 40.4 J .
(b) Then we find the final velocity from equation (1),
ω_f = [2W_T/I]^½ .
According to the table of Moments of Inertia, I = ½MR² for a solid cylinder. So

ω_f = [4W_T/MR²]^½ = 6.10 rad/s .
Suppose that there is friction in problem 12 and that the compression must in fact be 0.425 m for the block to just reach the top of the hill. What work is done by the frictional force?

Friction is a nonconservative forces so W_NC = W_friction ¹ 0. Thus

W_friction = mgh - ½Kx² = -132 J .

Friction does -132 Joules of work.

A large cylinder of mass M = 150 kg and radius R = 0.350 m. The axle on which the cylinder rotates is NOT frictionless. A rope is wrapped around the cylinder exactly ten times. From rest, the rope is pulled with a constant tension of 25.0 N. The rope does not slip and when the rope comes free, the cylinder has a forward angular velocity _f = 10.5 rad/s. The moment of inertia of a cylinder is I = ½MR².
(a) What angle was the cylinder rotated through?
(b) What is the frictional torque of the axle?
(c) How long will it take the frictional torque to bring the cylinder to a stop?
(d) How many revolutions will it have turned?

(a) Since the rope does not slip, the cylinder rotates ten times so Δφ = -20π, where the rotation is assumed to be clockwise.

(b) Since the problem involves forces and a change is rotational speed, we make use of the Generalized Work-Energy Theorem. Since there is only a change in rotational kinetic energy,
W_NC = ΔE = K_f - K_i = ½I[(ω_f)² - (ω₀)²] = ½I(ω_f)² .
The nonconservative forces in this problem are the tension and the axle friction, W_NC = W_T + W_f. So we have

W_T + W_f = ½I (ω_f)² . (1)
The definition of work in rotational situations is W = τΔφ. Tension is always tangential to cylinders so τ_T = -RT, again assuming the rope pulls the cylinder clockwise. Thus the work done by the tension is

W_T = (-RT)(-20π) = (0.35 m)(25 N)(20) = 549.78 J .
Using this result and equation (1), we can find the work done by friction

W_f = ½I(ω_f)² - W_T = ¼M(R_f)² - W_T = 506.46 J - 549.78 J = -43.3178 J .
Since W_f = τ_f Δφ, we find the frictional torque to be
τ_f = W_f / Δφ = W_f / -20π = +0.6894 Nm ;
the sign indicating that it is counterclockwise.

(c) After the rope comes off the cylinder, the only force acting is friction so the generalized Work-Energy Theorem becomes

W_f = ΔE = K_f - K_i = ½I[(ω_f) ² - (ω₀)²] = -½I(ω₀)² ,
where ω₀ here is ω_f from the first part of the problem and the new ω_f = 0 since the drum comes to a stop. Again W_f = τ_fΔφ, where τ_f is the result from part (b). Therefore
τ_fΔφ = -½I(ω₀)² = -(506.46 J) / 0.6894 Nm = -734.6 rad = 117 rev clockwise.
(d) To find the time it takes to slow down, note that we have the initial and final angular velocities and the angular displacement. Referring to our kinematics equations, we find
Δφ = ½(ω_f + ω₀)t.
Rearranging for t yields,
t = 2Δφ / (ω_f + ω₀) = 140 s .
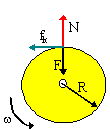
A person with an axe to grind is using a whetstone. The whetstone is connected to a motor which keeps it rotating at 85 rev/min. The whetstone is a solid cylinder of made of a special type of stone of mass 45 kg and radius 20 cm. The heavy axe-blade is being pressed onto the whetstone with a steady force of 25 N directed into the centre of the whetstone. Suddenly, the power to the motor is cut but the person maintains the force of the axe on the whetstone. The coefficient of kinetic friction between the axe and the stone is 0.60. The moment of inertia of a cylinder about it's centre of mass is I = ½MR².
(a) Calculate the torque of the frictional force on the wheel.
(b) Calculate the total angle through which the wheel turns from the time the power goes off to the time the whetstone stops rotating.
(c) How long does it take for the wheel to stop after the power outage?

(a) The frictional force is tangential to the surface of the whetstone. The friction torque is τ_f = Rf_k. The frictional force is given by f_k = μN. According to Newton's Third Law, the normal is equal to the force pressing the axe into the whetstone. Hence
τ_f = RF = (0.2 m)(0.6)(25 N) = 3.0 Nm .
(b) Since the object is rotating and we are given speeds, we apply the generalized Work-Energy Theorem. Note that we only have rotational kinetic energy, so
W_NC = ΔE = K_f - K_i = ½I[(ω_f) ² - (ω₀)²] = -½I(ω₀)² = -¼M(Rω₀)²,
where W_NC is the work done by friction in slowing the whetstone and we used the given I. The angular velocity is given in rev/min but in SI units it is

ω₀ = 85 rev/min × (2π rad)/rev × min/(60 s) = 8.9012 rad/s .
The definition of work is W_NC = τ_f Δφ. If we use this relation, we find that

Δφ = -¼M(R₀)² / τ_f = -¼(45 kg)(0.20 × 8.9012 rad/s)² / τ_f = 11.9 rad = 1.89 rev .
(c) To find the time it takes to slow down, note that we have the initial and final angular velocities and the angular displacement. Referring to our kinematics equations, we find
Δφ = ½ (ω_f + ω₀)t .

Rearranging for t yields,

t = 2Δφ / ω₀ = 2(11.88 rad)/(8.9012 rad/s) = 2.67 s .

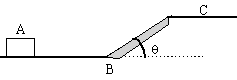
In the figure below, a block of mass 5.0 kg starts at point A with a speed of 15.0 m/s on a flat frictionless surface. At point B, it encounters an incline with coefficient of kinetic friction μ_k= 0.15. The block makes it up the incline to a second flat frictionless surface. What is the work done by friction? What is the velocity of the block at point C? The incline is 2.2 m long at an angle θ = 15°.

The problem involves a change in height and speed, so we apply the generalized Work-Energy Theorem.

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) = ½m(v_C)² - ½m(v_A)² + mgh . (1)

Here the nonconservative force is friction, so W_NC = W_f. To find friction, a force, we draw a FBD and use Newton's Second Law.

	i	j
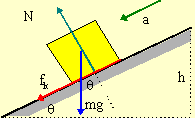	ΣF_x = ma_x	ΣF_y = ma_y
	-f_k - mgsinθ = -ma	N - mgcosθ = 0

The second equation gives N = mgcosθ and we know f_k = μ_kN, so f_k = μ_kmgcos θ. Therefore, the work done by friction is

W_f = -f_kΔx = -μ_kmgcosθΔx = -(.15)(5 kg)(9.81 m/s²)cos(15º)(2.2 m) = -15.635 J.

Note from the diagram, that the height h is related to the length of the incline by h = Δxsinθ. Putting both results into equation (1) yields

W_f = ½m(v_C)² - ½m(v_A)² + mg[Δxsinθ] .

Solving for v_C yields

v_C = [2W_f/m - 2gΔx sinθ + (v_A)²] ^½ = 14.4 m/s .

In the diagram block M₁ is connected to M₂ by a very light string running over three identical pulleys. The pulleys are disks with mass M_p and the rope does not slip. The coefficient of kinetic friction for the horizontal surface that M₁ is on is μ_k. Find an expression for the speed v of block M₂ in terms of the distance L that block M₁ moves to the right. Your answer should be expressed in terms of L, M₁, M₂, M_p, μ_k, and g only. Hint: work and energy methods provide the quickest solution.

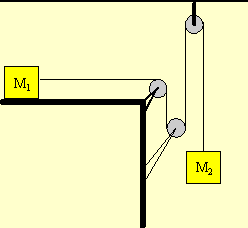
The problem involves changes in height, speed, and rotation, so we would apply the generalized Work-Energy Theorem even if not directed to do so,

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) , (1)

where K is the sum of all the linear and rotational kinetic energies of each object, and U is the sum of the gravitational potential energies. Since there is kinetic friction acting on the system, W_NC = W_f. To find W_f, we need to the frictional force. To find a force, we draw a FBD and use Newton's Second Law.

	i	j
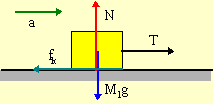	ΣF_x = ma_x	ΣF_y = ma_y
	T - f_k = M₁a	N - M₁g = 0

The second equation gives N = M₁g and we know f_k = μ_k N, so f_k = μ_kM₁g. Therefore, the work done by friction is W_f = -f_k Δx = -μ _kM₁gΔx.

Next consider the change in energy of each object. M₁ increases its linear kinetic energy. M₂ also increases its linear kinetic energy but loses gravitational potential energy. The three identical pulleys increase their rotational kinetic energies. Thus equation (1) becomes

-μ_kM₁gΔx = ½M₁v² + ½M₂v² - M₂gh + 3×½I_disk ω² .

Since M₁ and M₂ are connected by the same rope, they have the same speed and move the same distance so that Δx = h. Consulting a table of Moments of Inertia, we find I_disk = ½M_PR². Since the rope does not slip, the tangential speed of the pulleys is the same as the rope and thus ω = v/R. Substituting this relations back into our equation yields,

-μ_kM₁gh = ½M₁v² + ½M₂v² - M₂gh + 3×½[½M_PR²] (v/R)² .

Collecting the terms with v yields

½[M₁ + M₂ + (3/2)M_P] v² = [M₂ - μ _kM₁]gh .

Solving for v yields,

v = [2(M₂ - μ _kM₁)gh / (M₁ + M₂ + (3/2)M_P)]^½ .

Tarzan, Lord of Apes, is swinging through the jungle. In the diagram below, Tarzan is standing at point A on a tree branch h₁= 22.0 m above the floor of the jungle. Tarzan is holding one end of a vine which is attached to a branch on a second tree. The vine is L = 21.0 m long. When Tarzan swings on the vine, his path is in an arc of a circle. At the bottom of his swing he is at point B, 13.0 m above the ground . Ignore Tarzan's height. Tarzan has a mass of 90.0 kg. The vine does not stretch and has negligible mass.

(a) Why does the tension in the vine do no work?
(b) What will be his speed at this point?
(c) What will be the tension in the rope?

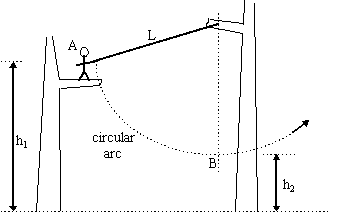
The problem involves a change in height and speed, so we apply the generalized Work-Energy Theorem.

W_NC = ΔE = (K_f - K_i) + (U_f - U_i) = ½m(v_B)² - mgh . (1)
(a) Here the only possible nonconservative force is friction, so W_NC = W_T. The definition of work is W = FΔxcosθ, but in this problem the tension is along a radius and is thus always at 90º to the displacement. As a result, W_T = 0. Thus we have
0 = ½m(v_B)² - mgh .
(b) To find the speed at point B, we need to know h, the distance Tarzan dropped. Examining the question, we see that h = h₁ - h₂ = 22.0 m - 13.0 m = 9.0 m. Rearranging our equation, we find
v_B = [2gh]^½ = [2(9.81 m/s²)(9 m)]^½ = 13.29 m/s .
(c) Tension is a force. To find a force we need to draw a FBD and apply Newton's Second Law. Since Tarzan is swinging in a circle, we are dealing with centripetal acceleration.

j

ΣF_y = ma_y

T - mg = mv²/L

Solving for T,

T = mg + mv²/L = (90.0 kg)[ 9.81 m/s² + (13.288 m/s)²/(21.0 m)] = 1.64 × 10³ N.
A block of mass M on a flat table is connected by a string of negligible mass to a vertical spring with spring constant K which is fixed to the floor. The string goes over a pulley that is a solid disk of mass M and radius R. As shown in the diagram below, the spring is initially in its equilibrium position and the system is not moving. A person pulls the block with force F through a distance L. Determine the speed v of the block after it has moved distance L.The tabletop is frictionless.

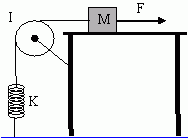
The problem involves changes in height, speed, and rotation, so we would apply the generalized Work-Energy Theorem even if not directed to do so,
Wext = ΔE, (1)
where E is the sum of all the mechanical energies of each object. If the system consists of the spring, string, pulley, block and the earth, then F is an external force acting on the system and Wext = FL.

Next consider the change in energy of each object. The spring stretches as so increases its potential energy. The pulley turns from rest so increases its rotational kinetic energy. The block moves from rest so it increases its linear kinetic energy. Thus equation (1) becomes
FL = ½Kx² + ½I_diskω² + ½Mv².
Since the block and spring are connected by the same string, the spring has stretched x = L. Consulting a table of Moments of Inertia, we find I_disk = ½MR². Since the string does not slip, the tangential speed of the pulleys is the same as the rope and thus ω = v/R. Substituting this relations back
FL = ½KL² + ½[½MR²](v/R)² + ½Mv² .
Collecting the terms with v yields

³/₄Mv2 = FL – ½KL2 .

Solving for v yields,

v = [(4M – 2KL²) / 3M]^½ .

What power is required to pull a 5.0 kg block at a steady speed of 1.25 m/s? The coefficient of friction is 0.30.

The power required to move the block at constant speed is P = Fv. We are given v, the speed of the block. To get F, a force, we draw a FBD and apply Newton's Second Law,

	i	j
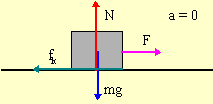	ΣF_x = ma_x	ΣF_y = ma_y
	F - f_k = 0	N - mg = 0

The second equation gives N = mg and we know f_k = μ_kN, so f_k = μ_kmg. Therefore, the applied force is F = μ_kmg. Thus the power is

P = μ_kmgv = (0.3)(5 kg)(9.81 m/s²)(1.25 m/s) = 18.4 Watts.

A 7500 W engine is propelling a boat at 12 km/h. What force is the engine exerting on the boat? What force and how much power is water resistance exerting on the speedboat?

First we convert the velocity to SI units,

12 km/h × (1000 m)/km × (1 h)/(3600 s) = 3.333 m/s .

We know P = Fv, so

F = P/v = 7500 W / 3.333 m/s = 2250 N .

By Newton's Third Law, the water is exerting 2250 N in the reverse direction. It is also removing 7500 W of power which is going into increasing the kinetic energy of the water.
A 3.0 hp engine pulls a 245-kg block at constant speed up a 12.0 m 30.0° incline. How long does this take? Ignore friction.

First, 3.0 hp × 746 W / hp = 2238 W.

Next, the work done by the engine must equal the work done by the weight, from Newton's Third Law. The work done by gravity is

W_gravity = mgh = mgLsinθ = 1.442 × 10⁴ J .
Since power is defined as work over time, P = W/t, the time it takes is

t = W/P = (1.442 × 10⁴ J) / (2238 W) = 6.44 s .

Questions? mike.coombes@kwantlen.bc.ca

	i	j
	ΣF_x = ma_x	ΣF_y = ma_y
	T - f_k - mgsinθ = ma	N - mgcosθ = 0

Force	Force (N)	φ	W = FΔxcosφ (J)
Tension	150	0	450
Weight	147.15	θ + π/2	-187
Normal	133.36	π/2	0
Friction	26.67	π	-80