![[Return to Physics Homepage]](./../../physics.gif)
![[Return to Mike Coombes' Homepage]](./../../coombes.gif)
![[Return to List of Handouts]](./../../handouts.gif)
![[Return to Problem Sets]](./../../problems.gif)
![[Return to List of Solutions]](./../../solutions.gif)
| Questions: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
A well-labeled sketch usually helps make the problem
clearer.

(a) The object is rotating and we are asked to find kinematic quantities, so this is a rotational kinematics problem.
ω0
= +5.0 rad/s
ωf
= -1.5 rad/s
Δθ = +5.5 rad
α = ?
ωaverage
= ?
t = ?
Note that I have taken counterclockwise as the positive
direction
and that the signs are explicitly stated. It is a very common
source of error to leave out or to not consider the signs of directions
of all vector quantities.
To find the angular acceleration, we find the kinematics
equation
that contains α and the
given quantities.
Examining our equations
we see that we can use  .
Rearranging this
equation to find α
yields
.
Rearranging this
equation to find α
yields  .
Notice that
the acceleration is negative. This means that the acceleration
points clockwise. It means that an object's rotation will slow,
stop, and reverse direction.
.
Notice that
the acceleration is negative. This means that the acceleration
points clockwise. It means that an object's rotation will slow,
stop, and reverse direction.
The average velocity is defined  .
.
To find the time, we find the kinematics equation that
contains
and t and the given quantities. Examining our equations we see that
we can use 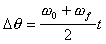 .
Rearranging this equation
to find t yields
.
Rearranging this equation
to find t yields  .
.
(b) When a rotating object changes its direction of
rotation,
we know that the object is instantaneously at rest and that its
velocity at that point is ω3
= 0. The information that
we have is thus:
ω0
= +5.0 rad/s
ω3
= 0 rad/s (This is our new final angular velocity)
α = -2.068 rad/s2
Δθ = ?
t = ?
Notice that the angular acceleration is a constant of the
motion;
it has the same value in both parts of the problem.
To find the displacement from the initial position where
the ball
reverses direction, we find the kinematics equation that contains
and the given quantities. Examining our equations we see that
we can use  .
Rearranging this equation
to find yields
.
Rearranging this equation
to find yields 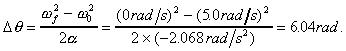 .
Notice that this value
is bigger than the original 5.5 rad and is consistent with the
sketch, i.e. the ball had rotated more when it turned around.
.
Notice that this value
is bigger than the original 5.5 rad and is consistent with the
sketch, i.e. the ball had rotated more when it turned around.
To find the time it takes for the ball to reach the point
where
it turns around, we find the kinematics equation that contains
t and the given quantities. Examining our equations we see that
we can use 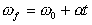 .
Rearranging this equation
to find t yields
.
Rearranging this equation
to find t yields 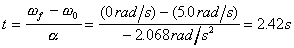 .
Notice that this value
is smaller than the time in part (a) and is consistent with the
sketch, i.e. the ball hasn't turned back yet.
.
Notice that this value
is smaller than the time in part (a) and is consistent with the
sketch, i.e. the ball hasn't turned back yet.
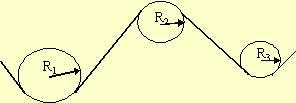
The object is rotating and we are asked to find kinematic quantities, so this is a rotational kinematics problem. The key physical point is that the speed of the belt and the tangential speeds of each pulley are the same since the belt does not slip,
Let's assume that the belt moves to the right. Since v =
ωR, ωn
= vbelt/Rn. So we have;
| Pulley 1 | Pulley 2 | Pulley 3 |
|---|---|---|
| ω1
= vbelt/R1 = (5.0 m/s)/(0.30 m) = 16.67 rad/s |
ω2
= vbelt/R2 = (5.0 m/s)/(0.20 m) = -25.0 rad/s (minus means clockwise) |
ω1
= vbelt/R1 = (5.0 m/s)/(0.10 m) = 50.0 rad/s |
| f1 = ω1/2π = 2.6526 s-1 | f2 = ω2/2π = 3.9789 s-1 | f3 = ω3/2π = 7.9577 s-1 |
| T1 = 1/f1 = 0.3770 s | T2 = 1/f2 = 0.2513 s | T3 = 1/f3 = 0.1257 s |
(b) For the increased belt speed, we can again use ωn = vbelt/Rn to get the new angular velocities of the three pulleys. With an initial and a final angular velocity and an elapsed time, we can find all the desired quantities using our kinematics equations:
ωaverage = ½(ωf + ω0), α = (ωf - ω0)/t, and Δθ = ωaveraget.
| Pulley 1 | Pulley 2 | Pulley 3 |
|---|---|---|
| ω1i = 16.67 rad/s | ω2i
= -25.0 rad/s (minus means clockwise) |
ω1i = 50.0 rad/s |
| ω1f
= vbelt/R1 = (10.0 m/s)/(0.30 m) = 33.3 rad/s |
ω2f
= vbelt/R2 = (-10.0 m/s)/(0.20 m) = -50.0 rad/s |
ω1f
= vbelt/R3 = (10.0 m/s)/(0.10 m) = 100.0 rad/s |
| ωaverage
1 = ½(ω1f
+ ω1i)
= 25.0 rad/s |
ωaverage
2 = ½(ω2f
+ ω3i)
= -37.5 rad/s |
ωaverage
3 = ½(ω3f
+ ω3i)
= 75.0 rad/s |
| α1
= (ω1f
- ω1i)/t = 1.67 rad/s2 |
α2
= (ω2f
- ω2i)/t = -2.50 rad/s2 |
α3
= (ω3f
- ω3i)/t = 5.00 rad/s2 |
| Δθ1
= ωaverage 1
× t = 250 rad = 39.8 rev |
Δθ2
= ωaverage 2
× t = -375 rad = -59.7 rev |
Δθ3
= ωaverage 3
× t = 750 rad = 119 rev |
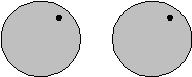
Since the disks are rotating and we are asked about
kinematic
quantities, this is a rotational kinematics problems. In particular,
since there are two objects, the is a two body or constrained
problem. To solve we sketch a graph of the angular displacement
versus time. The accelerating disk will have a curved versus t
line, while it is a straight line for the other disk. Examining
the graph will yield the desired constraints.
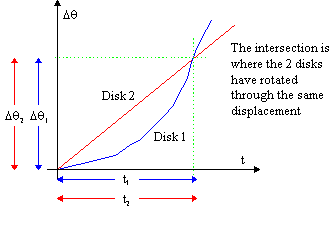
Inspecting the graph, we find that
We are given ω0 and α for each disk (recall that an object with constant velocity has a zero acceleration). We search for an equation which has the known quantities and the unknown quantities and t. This would be Δθ = ω0t + ½αt2. Our first constraint becomes
We can replace t2 by t1
in the equation
above by using our second constraint,
Plugging in our given quantities yields:
Solving for t1 gives the time it
takes for the dots
to line up, t1 = t2 =
3.00 s. Now that we
have time, we can find any other quantity. Plugging values into
Δθ = ω0t
+
½αt2,
yields Δθ1
= Δθ2
= 54.0 rad. This is how much each disk turns before they once
more line up.
To find the number of revolutions note that each revolution is 2π rad, so ω/2π = 8.59 revolutions. Each disk has turned 8.59 revolutions.
If the two disks had different radii, it would make no
difference
to our result. We were looking at rotational quantities, , , and
, which are independent of radius.
This problem is a combination of a rotational kinematics
problem
with a projectile motion problem. In both type one starts by listing
the given and requested quantities.
| i | j | rotation |
|---|---|---|
| v0x = 11.0 m/s cos(25) = 9.9694 m/s | v0y = 11.0 m/s sin(25) = 4.6488 m/s | ω0 = 35.0 rad/s |
| ax = 0 | ay = -g = -9.81 m/s2 | α = 0 |
| Δx = 0 | Δy = 0 | = ? |
| t = ? | t = ? | t = ? |
Notice that Δy
= 0, since the ball returns to the same height.
Also α = 0 as the ball
is in the air - no force is making it change
its rotation. Time is the common factor for this problem. Note
that there is enough information in the j
column to determine
the time in air using Δy
= v0yt - ½gt2.
Since Δy = 0, this
reduces to t = 2v0y/g = 0.9478 s.
We then find ω using
Δθ = ω0t
+ ½αt2
= (35.0)(0.9478) = 33.17 rad.
To convert from radians to revolutions, recall that 1
revolution
= 2π radians. Hence
ω= 33.17 / 2π
= 5.28 revolutions.
The ball rotates 5.28 times.
Converting from rpm to rad/s
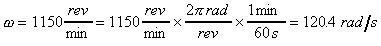 .
.The frequency is given by f = ω/2π =
19.2 s-1, and the
period is given by T = 2π/ω
= 0.0522 s.
The physical point here is that the linear speed of the
motorcycle
is equal to the tangential speed of the motorcycle's wheels,
where vTangential = Rwheel = 120.4 rad/s 0.22 m = 26.5 m/s. The motorcycle's speed is 26.5 m/s or 95.4 km/h.
As shown in the diagram below, the pedal gear has a radius
of
12.0 cm, the back wheel gear has a radius of 3.5 cm, and the
back wheel itself has a radius of 38.0 cm.
Since we are dealing rotational variables, this
is a rotational kinematics problem. The important physical principles
at work here are:
Thus we can relate all the requested quantities to
ωpedal final,
Δθpedal,
and αpedal.
Since we don't know Δθpedal
and αpedal,
we
will use our kinematics equation to find them. First we list our
known and desired quantities, converting rev/min to rad/s along
the way:
| ω0 = 30 rev/min = π rad/s | There are 2π rad per revolution |
| ωf = 120 rev/min = 4π rad/s | |
| t = 5.0 s | |
| αpedal = ? | |
| Δθpedal = ? |
We find αpedal
= (ωf
- ω0)/t
= 1.885
rad/s2 and Δθpedal
= ½(ωf
+ ω0)t
= 39.27 rad.
(a) Examining the relationships noted above,
Using our given radii, abike =
0.38(0.12/0.035)1.885
= 2.456 m/s2.
(b) We will find the same general result for the final linear speed of the bike,
(c) We also find the same general result for the final linear displacement of the bike,
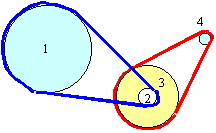
For Wheel 1, we can find 1,
We must relate the rotation of Wheel 4 to Wheel 1 via the intermediate Wheels. First Wheels 1 and 2 share a belt, so
| ΔS1 = ΔS2 or R1Δθ1 = R2Δθ2 . | (1) |
Thus we have Δθ2 = (R1/R2)Δθ1.
Wheels 2 and 3 share a common axle, so
| Δθ3 = Δθ2. | (2) |
Which means Δθ3 = (R1/R2)Δθ1.
Finally, Wheels 3 and 4 share a belt, so
| ΔS3 = ΔS4 or R4Δθ4 = R3Δθ3 . | (3) |
This yields Δθ4 = (R3/R4)Δθ3 = (R3/R4)(R1/R2)Δθ1 . Evaluating gives
Questions? mike.coombes@kpu.ca