Questions: 1 2 3

1. Round the following to the correct number of significant figures:
   (a) 71.85234 ± 0.02672     (b) 13.6 ± 0.210     (c) 0.0044667 ± 0.000081

Recall that we keep two digits if the first non-zero digit of the uncertainty is a 1 or a 2.

(a) 71.852 ± 0.027

(b) 13.60 ± 0.21

(c) 0.00447 ± 0.00008



---

2. Apply error propagation rules to the following:
   1. Let A = 79.5 ± 0.6, B = 27.8 ± 0.4, and C = 54.6 ± 0.3. Evaluate F = A - B + C.
      

      First we determine the principle value,
      

      P(F) = P(A) - P(B) + P(C) = 79.5 - 27.8 + 54.6 = 106.3 .

      Using the rule for addition and subtraction, the uncertainty is given by
      

      δ(F)	= δ(A - B + C)
      	= [(δA)2 + (δB)2 + (δC)2]½
      	= [(0.6)2 + (0.4)2 + (0.3)2]½
      	= 0.78

      Thus F = 106.3 ± 0.78 = 106.3 ± 0.8 .
      

   2. Let A = -12.1 ± 0.2 and B = 3.45 ± 0.06. Evaluate F = A/B.

      First we determine the principle value,
      

      P(F) = P(A)/P(B) = -12.1/3.45 = -3.5072 .

      Using the rule for multiplication and division, the uncertainty is given by
      

      δ(F)	= δ(A/B)
      	= P(A/B)[(δ(A)/P(A))2 + (δ(B)/P(B))2]½
      	= P(F)[(δ(A)/P(A))2 + (δ(B)/P(B))2]½
      	= |-3.5072|×[(0.02 / -12.1)2 + (0.06 / 3.45)2]½
      	= 0.0841

      Thus F = -3.5072 ± 0.0841 = -3.51 ± 0.08 .
      

   3. Let A = 15.4 ± 0.2, B = 7.85 ± 0.03, and C = 6.24 ± 0.08. Evaluate F = A /(BC).
      

      First we determine the principle value,
      

      P(F) = P(A/BC) = 15.4/(7.85 × 6.24) = 0.3144 .
      

      Using the rule for multiplication and division, the uncertainty is given by
      

      δ(F)	= δ(A/BC)
      	= P(F)[(δ(A)/P(A))2 + (δ(B)/P(B))2 + (δ(B)/P(B))2]½
      	= 0.3144×[(0.2 /15.4)2 + (0.03/7.85)2 + (0.08/6.24)2]½
      	= 0.00586

      Thus F = 0.3144 ± 0.0058 = 0.314 ± 0.006 .
      

   4. Let R = 0.151 ± 0.005. Evaluate V = (4/3)R³.
      

      First we determine the principle value,
      

      P(V) = (4/3)P(R³) = (4/3)(0.151)³ = 0.01442 .

      Using the rule for roots and powers, the uncertainty is given by
      

      δ(V)	= (4π/3)δ(R3)
      	= (4π/3)(3)[P(R)]2δ(R)
      	= 4π(0.151)2(0.005)
      	= 0.00143

      Thus V = 0.01442 ± 0.00143 = 0.014 ± 0.001 .
      

   5. Let X = 14.75 ± 0.09. Evaluate Y = 3X^½.

      First we determine the principle value,
      

      P(Y) = 3P(X^½) = 3(14.75)^½ = 11.522 .

      Using the rule for roots and powers, the uncertainty is given by
      

      δ(Y)	= 3δ(X½)
      	= 3(½)[P(X)]-½δ(X)
      	= (3/2)(0.09)/(14.75)½
      	= 0.035

      Thus Y = 11.522 ± 0.035 = 11.52 ± 0.04 .
      

   6. Let θ = 27.5 ± 0.5°. Evaluate Y = sin(θ).

      First we determine the principle value,
      

      P(Y) = P{sin(θ)} = sin(27.5°) = 0.46175 .

      Using the rule for functions, the uncertainty is given by
      

      δ(Y)	= δ{sin(θ)}
      	= δθ cos(P(θ))
      	= (0.5° × π/180°)cos(27.5)
      	= 0.00774

      Thus Y = 0.46175 ± 0.00774 = 0.462 ± 0.008 .

   7. Let λ = 3.51 ± 0.06. Evaluate N = e^-λ

      First we determine the principle value,
      

      P(N) = P(e^-λ) = e^-3.51 = 0.029897.
      

      Using the rule for functions, the uncertainty is given by
      

      δ(N)	= δ(e-λ)
      	= δλP(e-λ)
      	= (0.06)(0.029897)
      	= 0.00179

      Thus N = 0.029897 ± 0.00179 = 0.030 ± 0.002 .

   8. Let x = 0.75 ± 0.03. Evaluate φ = arctan(x).

      First we determine the principle value,

      P(φ) = arctan(0.75) = 36.870° or 0.64350 rad.

      Since we are dealing with a function

      δφ = δx / (1 + x²) = 0.03 / (1 + 0.75²) = 0.019 radians or δφ = 1.1°.

      Thus, φ = 36.9 ± 1.1° or φ = 0.644 ± 0.019 rad.

   

   ---

3. Find algebraic expressions for the absolute error in the following:
   

   (a)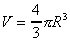

   R = 3.22 ± 0.04

   First let A = R³. Using the power rule, δA/A = 3δR/R.

   Thus V = (4π/3)A, where 4π/3 is a constant. So

   δV	= (4π/3)δA
   	= (4π/3)(R3)(3δR/R)
   	= 4πR2δR

   Evaluating we find V = 139.85 ± 5.21 = 140 ± 5 .

   (b)

   x = 2.25 ± 0.04, y = 3.72 ± 0.04

   First let A = x². Using the power rule, δA = 2xδx. Evaluating A = 5.0625 and δA = 0.18 .

   Similarly, let B = x². Evaluating this gives B = 13.8384. The uncertainty formula is δB = 2yδy which has the value δB = 0.2976 .

   Next let C = A + B. This is C = 18.9009 . Using the addition rule, we find

   δC	= [(δA)2 + (δB)2]½
   	= [(0.18)2 + (0.2976)2]½
   	= 0.3478

   Now we have z = C^½ or z = 4.3475. Using the power rule,

   δz	= ½δC / C½
   	= ½(0.3478)/4.3475
   	= 0.04

   Evaluating we find z = 4.35 ± 0.04 .

   (c)

   R = Acos(θ)

   A = 4.27 ± 0.07 θ = 35.0 ± 0.9°

   First let X = cos(θ). The pricipal value is X = 0.81915. Using the rule for functions δX = δθsin(θ) where δθ must be given in radians. Since δθ = 0.9° × π/180° = 0.01571, δX = 0.009010 .

   Now we have R = AX. Evaluating this gives R = (4.27)(0.81915) = 3.49777. Using the rule for multiplication to find the uncertainty yields

   δR/R	= [(δA/A)2 + (δX/X)2]½
   	= [(0.07/4.27)2 + (0.009010/0.81915)2]½
   	= 0.01980

   Cross-multiplying to find δR, we get δR = 3.49777(0.01980) = 0.06927 .

   The result is R = 3.50 ± 0.07 .

   (d)

   d = v0 + at

   v0 = 12.4 ± 0.2, a = −3.51 ± 0.11, t = 2.52 ± 0.08

   Let Y = at. The principle value is Y = (−3.51)(2.52) = −8.8452 . To find the uncertainty we use the multiplication rule.

   δY	= Y [(δa/a)2 + (δt/t)2]½
   	= (−8.8452)[(0.11/−3.51)2 + (.08/2.52)2]½
   	= −0.39457
   	= 0.39457

   Note that uncertainties are always positive.

   Now we are left with a simple sum, d = v₀ + Y. The principle value is d = 12.4 + −8.8452 = 3.5548. Using the addition rule for the uncertainty we find

   δd	= [(δv0)2 + (δY)2]½
   	= [ (0.2)2 + (0.39457)2]½
   	= 0.4424

   Thus we find v = 3.5548 ± 0.4424 = 3.6 ± 0.4 .

   (e)

   X = R tan2(θ)

   R = 6.85 ± 0.12 θ = 33.0 ± 0.8°

   Let A = tan(θ). The principle value is A = 0.64941 . Using the rule for the uncertainty in this function, δA = δθ / cos²(θ). Recall that δθ must be used in radians. So δθ = 0.8° × π/180° = 0.013963 . The uncertainty is δA = (0.013963)/cos²(33°) = 0.019851 .

   We now have X = RA², so let B = A². This has principle value B = 0.42173 . The rule for this power function yields the uncertainty δB = 2AδA with value δB = 2(0.64941)(0.019851) = 0.025783 .

   So we are left with X = RB. This has principle value X = (6.85)(0.42173) = 2.88885 . Using the rule for multiplication to find the uncertainty

   δX	= X [(δR/R)2 + (δB/B)2]½
   	= (2.88885)[(0.12/6.85)2 + (0.025783/0.42173)2]½
   	= 0.18372

   Thus we have X = 2.89 ± 0.18 .

   (f)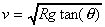

   R = 6.85 ± 0.12, g = 9.81 ± 0.01, θ = 43.0 ± 0.8°

   Let A = tan(θ) which has principle value A = 0.93252 . Using the rule for this function, δA = δθ /cos²(θ) where δθ must be in radians. Evaluating δA = (0.8° × π/180°)/cos²(43°) = 0.026104 .

   We now have v = [RgA]^½, so let B = RgA. The principle value is B = (6.85)(9.81)(0.93252) = 66.6639 . The uncertainty propagation rule for this multiplication yields

   δB	= B [(δR/R)2 + (δg/g)2 + (δA/A)2]½
   	= (66.6639)[(0.12/6.85)2 + (0.01/9.81)2 + (0.026104/0.93252)2]½
   	= 2.2025

   So now v = B^½ which, when evaluated, yields v = (66.6639)^½ = 8.16480 . The rule for the uncertainty in this function is

   δv	= ½δB / B½
   	= ½(2.2025)/(8.16480)
   	= 0.13488

   Thus we have v = 8.16 ± 0.13 .

   (g)

   d = v0t + ½at2

   v0 = 12.4 ± 0.2, a = −3.51 ± 0.11, t = 2.52 ± 0.08

   This is not a formula that we can work with. Suppose we let A = v₀t and B = ½at² so that d = A + B. We do not have a rule to find δd for this simple addition since δA and δB are not independent of one another since they both will include a δt dependence. We will have to wait until we can handle multivariate calculus to do this problem correctly.

   

Questions? mikec@kpu.ca