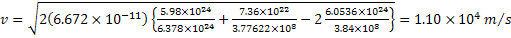[Return to Physics Homepage]     [Return to Mike Coombes' Homepage]     [Return to List of Handouts]     [Return to Problem Sets]     [Return to List of Solutions]

Questions: 1 2 3 4 5 6 7 8 9 10

Physics 1120: Gravitation Solutions

  1. Ted and Alice are mutually attracted to one another in the gravitational sense. If Ted's mass is 80.0 kg and Alice's is 55.0 kg and they are 0.150 m apart, what is the magnitude of the attraction on each? Treat them as point masses. What does this tell you about the gravitational effects of ordinary sized objects?

    Gravitational attraction is governed by the formula

    F = GM1M2 / R2 .

    Using the given values,

    F = (6.672 × 10-11 N-m2/kg2) (80 kg)(55 kg)/(0.15 m)2 = 1.30 × 10-5 N .

    This is a very small amount, so the gravitational force between normal sized object is negligible compared to the objects' weight.

    [Return to Top of Page]

  2. The distance between the centres of the earth and the moon is 3.85 × 108 m. The moon has a mass which is only 1.29% that of earth. Where would a satellite have to be placed to feel no net gravitational pull from the earth and the moon?

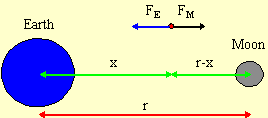
    There are two gravitational forces that an object would feel, FE and FM. Since there is no net force, we have

    FE - FM = 0 .            (1)

    Using the Law of Gravitation, this becomes

    GMEm / x2 = GMMm / (r-x)2 .

    Eliminating common factors yields

    ME / x2 = MM / (r-x)2 .

    Taking the square root of each side, we get

    [ME]½ / x = [MM]½ / (r-x) .

    Cross multiplying and rearranging,

    r-x = x [MM / ME]½ ,

    or , after we use the fact that MM = 0.0129 ME,

    r-x = (0.11358)x .

    Solving for x, we find

    x = r / [ 1 + 0.11358] = (3.85 × 108 m) / 1.11358 = 3.46 × 108 m .

    An object would have to be 3.46 × 108 m away from the earth, along a line from the earth to the moon, for the net gravitational pull to be zero.

    [Return to Top of Page]

  3. Given that the mass of the moon is 7.35 × 1022 kg, that the distance between the centres of the earth and the moon is 3.85 × 108 m, and that the radius of the earth is 6378 km, find the gravitational pull of the moon on a 75-kg person when the moon is directly overhead. Compare this to the person's weight (i.e. look at the ratio of the two).

    The force acting on the person is given by the Universal Law of Gravitation,

    F = GMMm / (Δr)2 ,

    where Δr = r - RE = 3.85 × 108 m - 6.378 × 106 m = 3.78622 × 108 m. Therefore the gravitational force from the moon is

    F = (6.672 × 10-11)(7.35 × 1022)(75)/(3.78622 108)2 = 2.57 × 10-3 N .

    The person's weight on the other hand is

    W = mg = (75 kg)(9.81 m/s2) = 736 N .

    The ratio of the two is

    F / W = (2.57 × 10-3) / 736 = 3.5 × 10-6.

    So the gravitational effect of even the nearest celestial body, the moon, is negligible comparing to the earth's gravitational pull on objects on its surface.

    [Return to Top of Page]

  4. The moon circles the earth once every 27.3 days. We have already determined that the mass of the earth is 5.98 × 1024 kg. What is the distance from the centre of the earth to the centre of the moon?

    From Kepler's Law, we know

    T = 2πR3/2 / [GMcentral]½ .

    If we rearrange this to find R, we get

    R = [GMcentralT2 / 4π2]1/3 .

    Next we convert the period into seconds

    T = (27.3 d) × (24 h) / (1 d) × (3600 s) / (1 h) = 2.3587 × 106 s .

    So we find the centre-to-centre distance radius to be

    R = [(6.672×10-11 N-m2/kg2) (5.98×1024kg)(2.3587×106 s)2 / 4π2]1/3 = 3.83 × 108 m .

    [Return to Top of Page]

  5. The earth is a satellite of the Sun. The distance from the sun to the earth is 1.50 × 1011 m. What is the mass of the Sun?

    From Kepler's Law, we know

    T = 2πR3/2 / [GMcentral]½ .

    If we rearrange this to find the mass of the Sun, we get

    Msun = 4π2 R3 / GT2 .

    Next we convert the period into seconds

    T = (365 d) × (24 h) / (1 d) × (3600 s) / (1 h) = 3.154 × 106 s .

    So we find the Sun's mass to be

    Msun = 4π 2(1.50×1011 m)3 / (6.672×10-11 N-m2/kg2) (3.154×106s)2 = 2.01 × 1030 kg .

    [Return to Top of Page]

  6. The brightest four moons of Jupiter were discovered by Galileo with one of his earliest telescopes. These moons, Io, Europa, Ganymede, and Callisto, are called the Galilean moons in his honour. Some of the available data about these moons are given below.
    MOON r (km) v T (earthyears)
    Io 4.219 × 105 - 0.004837
    Europa 6.712 × 105 - -
    Ganymede - - 0.0195884
    Callisto 1.853 × 106 - -
    The radii are from the centre of Jupiter to the centre of the moon in question. One earth year has 365 days. From the above data, determine (a) the mass of Jupiter, (b) the period of Europa, (c) the distance between Jupiter and Ganymede, and (d) the speed of Callisto.

    (a) Using Kepler's Law, and the data for Io, we can find the mass of Jupiter,

    MJupiter = 4π 2(RIo)3 / G(TIo)2 .

    First note that one year is

    Tyear = (365 d) × (24 h) / (1 d) × (3600 s) / (1h) = 3.154 × 106 s .

    So Io's period is

    TIo= 0.004837 × Tyear = 1.526 × 104 s .

    So the mass of Jupiter is

    MJupiter = 4π2 (4.219×108 m)3 /(6.672×10-11N-m2/kg2) (1.526×104 s)2 = 1.9097×1027 kg .

    (b) Now that we have the mass of Jupiter, we can find the period of Europa,

    TEuropa = 2π(REuropa)3/2 / [GMJupiter]½ .

    Using the given values,

    TEuropa = 2π (6.712×108)3/2 / [(6.672×10-11)(1.9097×1027)]½ = 3.061 × 105 s .

    In earth years, this is

    Teuropa = (3.061 × 105 s) × (1 year) / (3.154 × 106 s) = 0.009706 y .

    (c) We find the orbital radius of Ganymede using,

    RGanymede = [GMJupiter(TGanymede)2 / 4π2]1/3 .

    Ganymede's period is

    TGanymede= 0.0195884 × Tyear = 6.1782 × 104 s.

    Thus

    RGanymede = [(6.672×10-11) (1.9097×1027)(6.1782×104)2 / 4π2]1/3 = 1.072 × 106 km.

    (d) The orbital velocity is given by the formula

    VCallisto = [GMJupiter / RCallistor]½ .

    Using the given data, we find

    VCallisto = [(6.672×10-11) (1.9097×1027) / (1.853×106)] ½ = 8292 m/s .

    Callisto's orbital speed is 2.985 × 104 km/h.

    [Return to Top of Page]

  7. The mass of the planet Mercury is 3.30 × 1023 kg and its radius is 2.439 × 106 m. What would a 65.0-kg person weigh on Mercury?

    Weight is the gravitational attraction of the planet which can be found from The Universal Law of Gravitation,

    W = GMMercuryMperson / R2 .

    Using the given values,

    W = (6.672×10-11 N-m2/kg2) (3.30×1023 kg)(65 kg)/(2.439×106 m)2 = 241 N .

    We could have taken a slightly different route to the same answer by first calculating the acceleration due to gravity on Mercury's surface using

    gmercury = GMMercury / R2 .

    Using the given values,

    gmercury = (6.672×10-11 N-m2/kg2)(3.30×1023 kg) /(2.439×106 m)2 = 3.70 m/s2 .

    The person's weight is then

    W = Mpersongmercury = (65.0 kg)(3.70 m/s2) = 241.0 N .

    [Return to Top of Page]

  8. You wish to send a rocket from the surface of the earth to a point halfway between the centres of the earth and the moon. At that point it should have zero velocity. What initial speed must the rocket have to accomplish this feat? You must consider the potential energy of the rock with respect to both the earth and the moon. The centre to centre earth-moon distance is 3.84 × 108 m. The radius of the earth is 6378 km. The mass of the earth is 5.98 × 1024 kg and the moon has a mass of 7.36 × 1022 kg.

    To a very good approximation, we need only consider kinetic and potential energies, so that this is a Conservation of Energy problem,

    Kf + Uf = Ki + Ui ,            (1)

    where U is the total potential energy of the rocket with respect to both the moon and the earth. Thus the potential energy is

    U = -GMEm / r1 - GMMm / r2 ,            (2)

    where r1 is the rocket's distance from the centre of the earth and r2 is the distance to the centre of the moon.

    If we call the distance between the earth and the moon d, then r1f = r2f = ½d, and r1i = RE, and r2i = d - RE. Equation (1) thus becomes

    -GMEm/(½d) - GMMm/(½d) = ½mv2 - GMEm/RE - GMMm/(d - RE) .

    The common factor, m, cancels. Solving for v yields,

    v = [2G{ME/RE + MM/(d-RE) - 2(ME+MM)/d}]½ .

    Now

    d - RE = 3.84 × 108 m - 6.378 × 106 m = 3.77622 × 108 m , and

    ME + MM = 5.98 × 1024 kg + 7.36 × 1022 kg = 6.0536 × 1024 kg ,

    using the given values

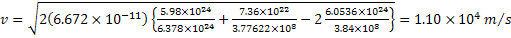
    [Return to Top of Page]

  9. A large star after is novas can collapse back into a superdense object call a neutron star. A large enough star can theoretically collapse back into a black hole. In the case of a neutron star light cannot escape from its surface because the pull of gravity is so great. For black holes, one talks of an event horizon below which light cannot escape. If the neutron star (black hole) has a mass of 100 of our suns, what is the radius of the neutron star (event horizon)? Calculate the density of such a neutron star. The mass of our sun is 1.99 × 1030 kg and the speed of light is 3.0 × 108 m/s.

    The escape velocity is given by the formula

    vescape = [2GMStar / RStar]½ .

    This can be rearranged to give

    RStar = 2GMStar / (vescape)2 .

    Using the given values,

    RStar = 2(6.672×10-11 N-m2/kg2)(100)(1.99×1030 kg) / (3.0×108 m/s)2 = 295 km .

    The density of an object is the ratio of its mass to its volume. The neutron star is spherical, so

    V = 4π(RStar)3/3 = 4π(2.95 × 106 m)3 / 3 = 1.0759 × 1017 m3 .

    Thus the density of the neutron star is

    D = M / V = (100)(1.99×1030 kg) / (1.0759 × 1017 m3) = 1.85 × 1015 kg/m3 ,

    This is approximately a trillion times denser than water which has a density of 1000 kg/m3 .

    [Return to Top of Page]

  10. At perigee, the point of closest approach, a satellite moves with 3 times the speed that it has at apogee, the point of greatest separation. At perigee it is 1000 km above the surface of the earth. The mass of the earth is 5.98 × 1024 kg and it's radius is 6378 km.
    (a) How far away is it at apogee? Hint: consider the angular momentum at apogee and perigee.
    (b) What is the speed of the satellite at perigee and apogee?

    (a) In the absence of external torques, the angular momentum of the system is conserved.

    Lapogee = Lperigee .            (1)

    At both points the velocity is perpendicular to the radius, so the L = mvR. Equation (2) becomes

    mvapogeeRapogee = mvperigeeRperigee .

    We are told that vperigee = 3vapogee. Using this and eliminating the common factor m, we find

    Rapogee / Rperigee = vperigee / vapogee = 3 .

    Thus

    Rapogee = 3Rperigee = 3(1000 km + 6378 km) = 22100 km .

    (b) In the absence of external forces, the total energy of the system is conserved.

    ½m(va)2 - GMEm/Ra = ½m(vp)2 - GMEm/Rp .            (2)

    We can eliminate the common factor m. We can also use Ra = 3Rp and vp= 3va, to simplify equation (2)

    ½(va)2 - GME/Ra = ½(3va)2 - GME/(Ra/3) .

    Collecting like terms and simplifying yields,

    va = [GME / 2Ra]½ = [(6.672×10-11)(5.98×1024) / 2(2.21×107)]½ = 3000 m/s.

    And vp = 3va = 9000 m/s.

    [Return to Top of Page]

[Return to Physics Homepage]     [Return to Mike Coombes' Homepage]     [Return to List of Handouts]     [Return to Problem Sets]     [Return to List of Solutions]

Questions? mike.coombes@kpu.ca

[Return to Kwantlen Homepage]