PHYS 1120 Waves Solutions

Questions: 1 2 3 4 5 6 7 8 9 10 11

Physics 1120: Waves Solutions

A wire of length 4.35 m and mass 137 g is under a tension of 125 N. What is the speed of a wave in this wire? If the tension is doubled, what is the speed? If the mass is doubled?

The speed of a wave on a string is given by the formula , where is the linear density given by 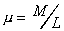. Thus the speed is

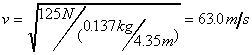If we double the tension, v = 89.1 m/s .

If we double the mass, v = 44.5 m/s .

A wave on a string has the formula y = 0.030sin(0.55x − 62.8t + π/3). What is the wavelength, frequency, period, phase constant, and speed of the wave. The string has a linear density μ = 0.020 kg/m. What is the tension in the string? What is the rate of energy flow of the wave? Sketch the reference circle, the snapshot graph at t = 0, and the history graph at x = 0.

First recall that the formula for a wave on a string is given by y = Asin(kx ± ωt + φ₀) Thus, by inspection, we have A = 0.030 m, , , 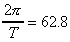and φ₀ = π/3. Solving for λ and T yields λ = 11.4 m and T = 0.100 s.

We know that frequency is given by f = 1/T = 10.0 Hz.

As well, the speed of the wave is given by v = λ/T = 114 m/s.

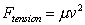To find the tension in the string, we take and rewrite it as. For the given values, F_tension = 260 N.

The rate of energy flow, or energy per unit time, or power, is given by the formula 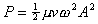, where ω = 2πf. For the given values, P = 4.05 Watts.

The phase constant puts the vector in the first quadrant.

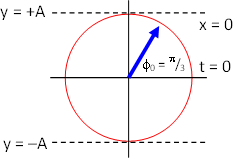
The snapshot graph, a plot of y versus x, for t = 0 can be sketched by referring to the phasor or reference circle diagram. The y-component of the amplitude is positive at x = 0, y = Asin(π/3) = 0.866A. As x increases, the phase 0.55x − 62.8t + π/3 also increases and the vector rotates counter clockwise to maximum y amplitude A. The snapshot graph therefore looks like:

The history graph, a plot of y versus t, for x = 0 can be sketched by referring to the phasor or reference circle diagram. The y-component of the amplitude is positive at t = 0, y = Asin(π/3) = 0.866A. As t increases, the phase 0.55x − 62.8t + π/3 decreases and the vector rotates clockwise to zero amplitude. The history graph therefore looks like:

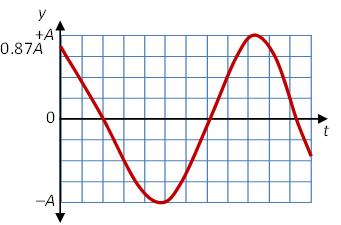
On a point on a string, a peak of a harmonic wave is observed to pass every 0.050 s. The distance between peaks is 0.75 m. The height of the peak is 0.025 m. Assume that the wave is moving to the left. What is the equation of this wave (take t = 0, x = 0 at the first peak)? What is the phase constant? What is the speed of the wave? The string has a linear density μ = 0.020 kg/m. What is the tension in the string? What is the rate of energy flow of the wave? Sketch the reference circle, the snapshot graph at t = 0, and the history graph at x = 0.

Since the peak of the harmonic wave is observed to pass every 0.050 s, T = 0.050 s. Since the distance between successive peaks is one wavelength, λ = 0.75 m. The amplitude of a wave is given by the height of the peak, so A = 0.025 m.

Next recall that the formula for a wave on a string is given by y = Asin(kx ± ωt + φ₀). For waves moving to the left, we need the + sign. Since we start with t = 0 and x = 0 at a peak, the phase constant φ₀ is π/2. So the required equation must be

y = 0.025sin(2πx/0.075 + 2πt/0.050 + π/2).

The speed of the wave is given by v = λ/T = 15.0 m/s.

From the previous question, we saw thatcould be rearranged to give. For the given values, F_tension = 0.045 N.

The rate of energy flow, or energy per unit time, or power, is given by the formula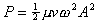, where ω = 2πf. For the given values, P = 0.296 Watts.

The phase constant puts the vector on the y-axis between the first and second quadrants.

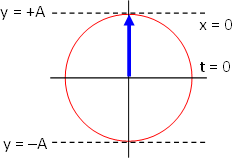
The snapshot graph, a plot of y versus x, for t = 0 can be sketched by referring to the phasor or reference circle diagram. The y-component of the amplitude is maximum, A. As x increases, the phase 8.38x + 126t + π also increases and the vector rotates counter clockwise to zero amplitude. The snapshot graph therefore looks like:

The history graph, a plot of y versus t, for x = 0 can be sketched by referring to the phasor or reference circle diagram. The y-component of the amplitude is maximum, A. As t increases, the phase 8.38x + 126t + π also increases and the vector rotates counter clockwise to zero amplitude. The history graph therefore looks like identical to the snapshot graph:

Sketch the associated snapshot and history graphs for the following reference circle diagrams. What is the phase constant φ₀ in each case?
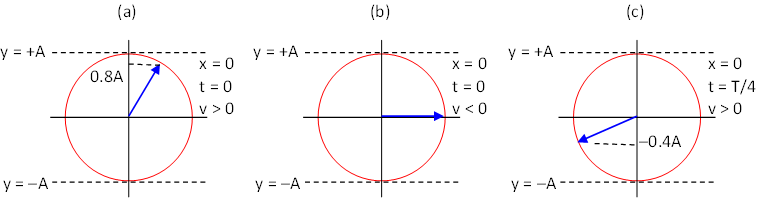
(a) The phase constant φ₀ is the angle measured counter clockwise from the positive x-axis to the vector when the diagram shows x = 0 and t = 0. Simple trigonometry indicates that φ₀ = arcsin(0.8) = 53.1° or 0.927 rad.
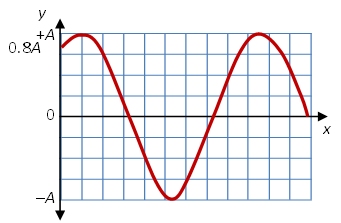
The vector in the phasor diagram rotates counter clockwise with increasing x in the y versus x, or snapshot graph. So here the y starts at 0.8A and rises to maximum amplitude A. The snapshot graph looks like.

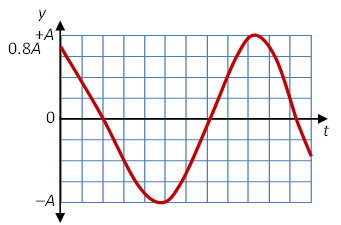
The vector in the phasor diagram rotates clockwise with increasing t in the y versus t, or history graph if the wave is moving to the right as it does here. So here the y starts at 0.8A and falls to equilibrium, zero amplitude. The history graph looks like.

(b) The phase constant φ₀ is zero.
Since the wave is moving to the left, the snapshot and history graphs look identical. The vector in the phasor diagram rotates counter clockwise with increasing x or with increasing t. The initial amplitude is zero and rises to a maximum.

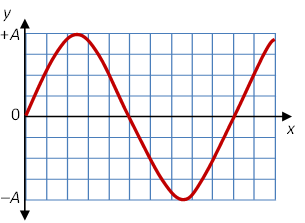
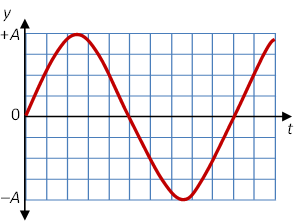
(c) Note that this phasor diagram is not given at t = 0 but at the later time t = T/4. The phase constant φ₀ is the angle measured counter clockwise from the positive x-axis to the vector when the diagram shows the vector at x = 0 and t = 0. Since this wave is moving to the right, the vector in the phasor diagram would have already moved one-quarter of the circle clockwise in this time (T/4 &rarrow; 2π/4). We need to rotate the vector back one-quarter of the circle counter clockwise to see what it would look like at t = 0. This is shown below.

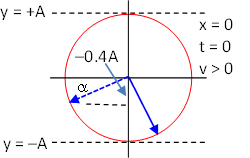
From the original information it is easy to determine the angle α = arcsin(0.4) = 23.58° = 0.412 rad. Thus the phase constant φ₀ = 180° + α + 90° = 293.58° or 5.124 rad. At x = 0 and t = 0, the amplitude is y = Asin(293.58°) = −0.917A. The vector in the phasor diagram will rotate counter clockwise with increasing x in the snapshot graph heading to zero amplitude. As the wave is travelling to the right, the vector in the phasor diagram will rotate clockwise with increasing t in the history graph heading to the minimum amplitude, −A. Both graphs are shown below.
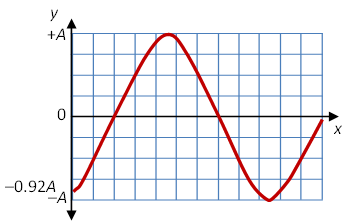
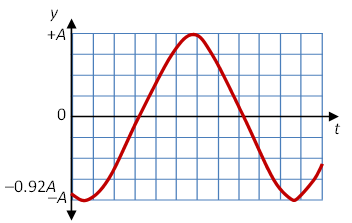
Consider the snapshot graph below for a wave moving to the right at t = 0. What is the phase constant φ₀? Sketch the reference circle at the indicated points A, B, C, and D. Where exactly does point A occur? Point B?

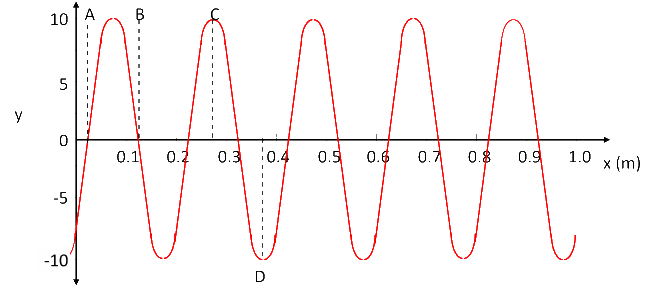
The phase constant φ₀ is the angle measured counter clockwise from the positive x-axis to the vector when the phasor diagram shows x = 0 and t = 0. The snapshot graph above shows that the initial amplitude is −7.5 or −0.75A where A = 10. The graph next has zero amplitude. Since the vector in a phasor diagram moves counter clockwise with increasing x, the vector must be in the fourth quadrant as shown in the diagram below.

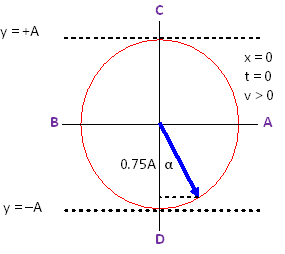
We can find the angle α in the phasor diagram, α = arccos(0.75) = 41.41° or 0.7227 rad. The phase constant is therefore φ₀ = α + 270° = 311.41° = 5.435 rad.

The locations of points A, B, C, and D are shown on the phasor diagram above.

To find the exact value of x for point A, note that one full rotation of the vector about the reference circle is equivalent to a shift of one wavelength λ on the snapshot graph. The vector needs to rotate counter clockwise 90° - α = 48.59° to get to point A. Therefore the location is x_A = (48.59° / 360°)λ. From the snapshot graph we can read that λ = 0.20 m. So x_A = 0.0270 m.

Similarly, to find the exact value of x for point B, the vector needs to rotate counter clockwise 90° - α + 180° = 228.59°. Therefore the location is x_B = (228.59° / 360°)(0.20) = 0.1270 m.

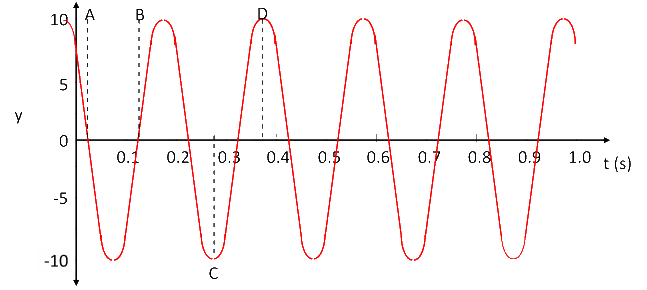
Consider the history graph below for a wave moving to the right at x = 0. What is the phase constant φ₀? Sketch the reference circle at the indicated points A, B, C, and D. When exactly does point A occur? Point B?

The phase constant φ₀ is the angle measured counter clockwise from the positive x-axis to the vector when the phasor diagram shows x = 0 and t = 0. The history graph above shows that the initial amplitude is 7.5 or 0.75A where A = 10. The graph next has zero amplitude. Since the vector in a phasor diagram moves clockwise with increasing t for a wave travelling to the right, the vector must be in the first quadrant as shown in the diagram below.

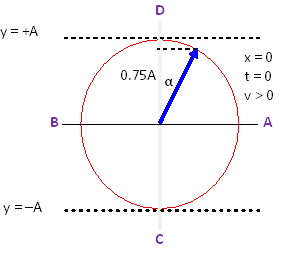
We can find the angle α in the phasor diagram, α = arccos(0.75) = 41.41° or 0.7227 rad. The phase constant is therefore φ₀ = 90° − α = 48.59° = 0.8481 rad.

The locations of points A, B, C, and D are shown on the phasor diagram above.

To find the exact value of t for point A, note that one full rotation of the vector about the reference circle is equivalent to a shift of one period T on the history graph. The vector needs to rotate clockwise 48.59° to get to point A. Therefore the time is t_A = (48.59° / 360°)T. From the history graph we can read that T = 0.20 s. So t_A = 0.0270 s.

Similarly, to find the exact value of t for point B, the vector needs to rotate clockwise φ₀ + 180° = 228.59°. Therefore the time is t_B = (228.59° / 360°)(0.20) = 0.1270 s.

Superposition in 1D and 2D

Two out-of-phase harmonic waves are traveling on a string. They each have an amplitude of 5.0 mm. The resultant wave has an amplitude of 3.5 mm. What is the phase difference between these two waves?

We saw that when two waves on a string interfere, we get another traveling wave whose amplitude is related to the amplitude of the original two waves by
.

This may be rearranged to yield
.

Using the given values, we find
.
Two speakers are in a line but one speaker is a distance d behind the other. You are 4.50 m in front of the nearest speaker. The sound is wavelength λ = 1.50 m.
(a) The speakers are in phase. What is the smallest non-zero d if you hear constructive interference?
(b) The speakers are in phase. What is the smallest non-zero d if you hear destructive interference?
(c) The front speaker leads the back speaker by 90°. What is the smallest non-zero d if you hear constructive interference?
(d) The front speaker leads the back speaker by 90°. What is the smallest non-zero d if you hear destructive interference?
(a) The equation for constructive interference is
δ = 2πΔx/λ + Δφ₀ = n2π            n = 0, 1, 2, 3, …            C.I.
The path difference Δx is d in this question and since the speakers are in phase Δφ₀ = 0. The above equation can be simplified to
d/λ = n            n = 0, 1, 2, 3, …            C.I.
The smallest non-zero d for constructive intereference occurs for n = 1, so d = λ = 1.50 m.
(b) Similarly the general equation for Destructive Interference is given by
δ = 2πΔx/λ + Δφ₀ = mπ            m = 1, 3, 5, …            D.I.
Simplifying again
2d/λ = m            m = 1, 3, 5, …            D.I.
The smallest non-zero d for destructive intereference occurs for m = 1, so d = ½λ = 0.75 m.
(c) Leading means the vector for the front speaker is 90° counter clockwise from the vector for the back speaker in the phasor diagram (shown below). For convenience, we can arbitrarily set the vectors at 90° and 0° in the phasor diagram. Since we draw a snapshot graph, the vectors in the phasor diagram rotate counter clockwise. The snapshot for the front speaker starts at maximum amplitude and will drop to zero. The back speaker starts at zero amplitude and rises to maximum. The diagram below shows the phasor diagram and the sound wave coming from each speaker but with the speakers shown side by side.

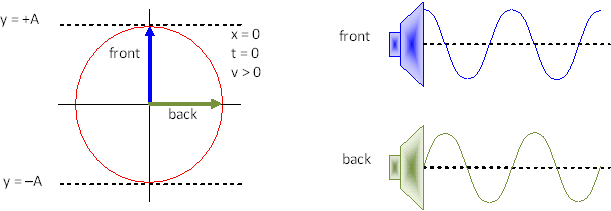
Clearly, the two waveforms will line up peak to peak, i.e. interfere constructively, when the back speaker is moved back ¼λ or d = 0.375 m.
(d) Similarly, the two waveforms will line up peak to trough, i.e. interfere destructively, when the back speaker is moved back ¾λ or d = 1.125 m.
Note in this problem, the location of the observor is irrelevant.
Two loudspeakers are located 3.00 m apart on the stage of an auditorium. A detector is placed 20.0 m from one speaker and 21.2 m from the other. A signal generator drives the two speakers in phase and sweeps through the range (2 KHz − 20 KHz). Assume that the speed of sound in air is 343 m/s.
(a) What is lowest note (frequency) for which destructive interference is a maximum?
(b) What is highest note for which destructive interference is a maximum?
(c) What is the lowest note for which constructive interference is a maximum?
(d) What is the highest note for which constructive interference is a maximum?

(a) & (b) Since the sounds are in phase, destructive interference occurs when the difference in position is an odd number of half wavelengths,
D.I.        Δx / λ = ½n,        where n = 1, 3, 5, …
The difference in position is Δx = 21.2 m − 20.0 m = 1.2 m. We can use the relation v = λf, to eliminate λ in favour of f. Thus we get
D.I.        f = nv / 2Δx = n(142.9 Hz),        where n = 1, 3, 5, …
We next need to find the smallest and largest odd values of n in the given range of frequencies of 2,000 to 20,000 Hz. We find n = 15 yields f = 2,144 Hz and n = 139 yields f = 19,865 Hz.

(c) & (d) Similarly, constructive interference occurs when the difference in position is an integral number of full wavelengths,
C.I.        Δx / λ = n,        where n = 0, 1, 2, 3, …
Using the difference in position is Δx = 1.2 m. and the relation v = λf, we get
C.I.        f = nv / Δx = n(285.8 Hz),        where n = 0, 1, 2, 3, …
We next need to find the smallest and largest values of n in the given range of frequencies of 2,000 to 20,000 Hz. We find n = 14 yields f = 2,001 Hz and n = 69 yields f = 19,722 Hz.
Two stereo speakers, driven by the amplifier so that the sources are in phase, are arranged so that the sound is loudest at your position. What is the minimum non-zero distance that you are farther away from one speaker than the other? The frequency of the tone from the speakers is 750 Hz and the speed of sound in air is 340 m/s.
Loudest means constructive interference is occurring. There is no phase difference so the equation for superposition is
δ = 2πΔx/λ = n2π            n = 0, 1, 2, 3, …            C.I.
We can make this an equation for frequency rather than wavelength by using the equation v = λf to eliminate λ in the equation above.
δ = 2πΔxf/v = n2π            n = 0, 1, 2, 3, …            C.I.
Rearranging to isolate Δx yields
Δx = nv/f            n = 0, 1, 2, 3, …            C.I.
The minimum non-zero distance occurs when n = 1, and we find Δx = 1 × (343 m/s) / (750 Hz) = 0.453 m.
As shown in the diagram below, a speaker plays a single frequency sound. On its way to you, some of the sound echoes (reflects) off a wall. As a result, the sound is quieter than it should be.
(a) If the wall is flexible, what is the lowest frequency that creates the lowest sound intensity at your position?
(b) If the wall is stiff, what is the lowest frequency that creates the lowest sound intensity at your position?

The speed of sound is 340 m/s. The lowest sound intensity occurs for destructive interference. If the wall is flexible, when the sound reflects the wave will not change phase. Thus the condition for destructive inference is

D.I. Δx / λ = ½n, where n = 1, 3, 5, …

We need to use the Pythagorean Theorem to get the difference in position, Δx = 2[(1.8 m) + (2.0 m)]^½ − 4.0 m = 1.381 m. We can use the relation v = λf, to eliminate λ in favour of f. Thus we get

D.I. f = nv / 2Δx = n(123 Hz), where n = 1, 3, 5, …

The lowest frequency is therefore 123 Hz.

Now if the wall is stiff, the phase of one wave is flipped, that is it is moved out of phase by one half wavelength. We must account for this initial difference

D.I. Δx / λ + ½ = ½n, where n = 1, 3, 5, …

Or in terms of frequency

D.I. f = ½[n - 1]v / Δx = [n - 1](123 Hz), where n = 1, 3, 5, …

Here the n = 1 gives an unphysical solution, and the lowest frequency occurs for n = 3 and is 246 Hz.

Questions? mike.coombes@kpu.ca