[Return to Physics Homepage]     [Return to Mike Coombes' Homepage]     [Return to List of Handouts]     [Return to Problem Sets]     [Return to List of Solutions]

Questions: 1 2 3 4 5 6 7 8 9 10

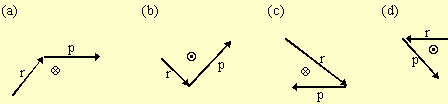
Physics 1120: Angular Momentum Solutions

  1. Determine the direction of the angular momentum for the following cases:

    Angular momentum is defined as the cross product of position and momentum, L = r × p. The direction of the angular momentum is perpendicular to the plane formed by the position and momentum vectors. For this problem that means either into the paper, denoted by ×, or out of the paper, (·). To find the direction, we sweep our right hand through the smallest angle formed by the vector. The way the thumb points indicates the direction of the angular momentum.

    [Return to Top of Page]

  2. Calculate the angular momentum for the following particles. Find the angle between the position and the momentum vectors.
    (a) r= (4, -5, 3) and p = (1, 4, -2)
    (b) r = (1, -2, 3) and p = (7, -1, 1)
    (c) r = (0, 2, 0) and p = (1, 0, 0)

    The angular momentum can be found either by evaluating the determinant or by using L = rpsinφ. We will use the first method to find L. We can find the angle between the momentum and position vectors using φ = sin-1(L/rp). We find the magnitudeof the vectors using the 3D form of the Pythagorean Theorem.

    (a)

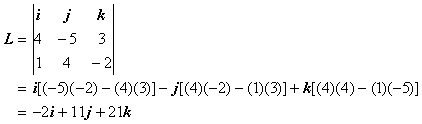
    L = [(-2)2 + (11)2 + (21)2]½ = 23.791 kg-m2/s

    r = [(4)2 + (-5)2 + (3)2]½ = 7.0711 m

    p = [(1)2 + (4)2 + (-2)2]½ = 4.5826 kg-m/s

    φ = sin-1(L/rp) = sin-1[ 23.791 / (7.0711 × 4.5826)] = 47.2°



    (b)

    L = [(1)2 + (20)2 + (13)2]½ = 23.875 kg-m2/s

    r = [(1)2 + (-2)2 + (3)2]½ = 3.7417 m

    p = [(7)2 + (-1)2 + (1)2]½ = 7.1414 kg-m/s

    φ = sin-1(L/rp) = sin-1[ 23.875 / (3.7417 × 7.1414)] = 63.3°


    (c)

    L = [(0)2 + (0)2 + (-2)2]½ = 2 kg-m2/s

    r = [(0)2 + (2)2 + (0)2]½ = 2 m

    p = [(1)2 + (0)2 + (0)2]½ = 1 kg-m/s

    φ = sin-1(L/rp) = sin-1[ 2 / (2 × 1)] = 90°

    [Return to Top of Page]

  3. Calculate the angular momentum of a phonograph record (LP) rotating at 331/3 rev/min. An LP has a radius of 15 cm and a mass of 150 g. A typical phonograph can accelerate an LP from rest to its final speed in 0.35 s, what average torque would be exerted on the LP?

    The angular momentum of a rotating body is L = IΩ. An LP is a solid disk. Consulting a table of moments of inertia, we find I = ½MR2. The angular velocity must be converted to rad/s

    Ω = 100/3 rev/min × 2π rad / rev × 1 min / 60 s = 3.4907 rad/s .

    Thus we find the angular momentum of the LP to be

    L = IΩ = ½MR2Ω = ½(0.15 kg)(0.15 m)2(3.4907 rad/s) = 5.8905 × 10-3 kg-m2/s .

    Torque is equal to the change in angular momentum with time

    τ = ΔL / Δt = (Lf - Li) / Δt = (5.8905 × 10-3 kg-m2/s - 0) / 0.35 s = 1.68 × 10-2 N-m .

    [Return to Top of Page]

  4. A cylinder of mass 250 kg and radius 2.60 m is rotating at 4.00 rad/s on a frictionless surface when two more identical non-rotating cylinders fall on top of the first. Because of friction between the cylinders they will eventually all come to rotate at the same rate. What is this final angular velocity?

    We have a collision that results in a change in rotation, so we conserve angular momentum,

    Lf = Li .            (1)

    The objects are rotating so their angular momentum is given by L = IΩ. Thus in this particular case, equation (1) becomes

    3IΩf = IΩi .

    Solving, we find

    ωf = Ωi / 3 = 1.33 rad/s .

    [Return to Top of Page]

  5. In a nightmare you dream that you are a hamster running in an exercise wheel. Typical hamsters are 300 g and can run at speeds of 3.2 m/s. A typical exercise wheel has a moment of inertia about its centre of 0.250 kg-m2. How fast should the wheel have been rotating in your dream? The radius of the wheel is 12.0 cm. Treat the hamster as a point mass. Hint what was the angular momentum of the system before the hamster started running?

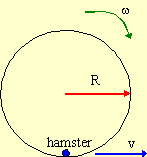
    Before the hamster starts running, the exercise wheel is not rotating. Considered as a system, angular momentum must be conserved.

    Lf = Li .

    For this particular problem,

    Lwheel + Lhamster = 0 .

    The wheel is a rotating object so its angular momentum is given by Lwheel = -IΩ , where the minus sign indicates that it is into the paper. For a point particle, the angular momentum is Lhamster = Rmv out of the paper. Thus we have

    -IΩ + Rmv = 0 .

    So the angular velocity of the wheel is

    Ω = Rmv / I = (0.3 kg)(0.12 m)(3.2 m/s) / (0.25 kg-m2/s) = 0.461 rad/s .

    [Return to Top of Page]

  6. A door with width L = 1.0 m and mass M = 15 kg is hinged on one side so that it can rotate freely. A bullet, as shown, is fired into the exact centre of the door. The bullet has mass 25 g and a speed of 400 m/s. What is the angular velocity of the door with respect to the hinge just after the bullets embeds itself in the door? The door may be treated as a thin rectangular sheet. The bullet may be treated as a point mass.

    Since we have a collision in which there is a change in rotation, we apply the Law of Conservation of Momentum,

    Lf = Li .           (1)

    Initially the bullet is traveling in a straight line so its angular momentum is bmv, where b is the distance of closest approach to the point of rotation. Since everything will rotate about the door hinge, we take the hinge as the point of rotation. Hence b = ½L. After the collision, the bullet is stuck in the door and rotates with the door in a circle. The angular momentum of an object moving in a circle is r2mΩ, where r is the radius of rotation. Clearly r = ½L.

    Initially the door is not rotating and thus has no angular momentum. Afterwards, it is rotating and thus has an angular momentum given by IΩ. Note that the door is not rotating about its centre of mass, so we need to use the parallel axis theorem. Consulting a table, we find Icm = (1/12)ML2. The centre of mass is d = ½L from the hinge.

    Thus equation (1) applied to this problem is

    (½L)2mΩ + [(1/12)ML2 + M (½L)2]Ω = ½Lmv .

    Dividing through by ½L and solving for Ω, we find

    Ω = mv / [½m + (2/3)M]L = (0.025)(400) / [½(0.025) + (2/3)15] = 0.999 rad/s .

    [Return to Top of Page]

  7. A 150-g piece of playdough slides across a frictionless table at v = 5.50 m/s. It collides with a disk of radius R = 35.0 cm and mass M = 2.50 kg which has a fixed frictionless axle. The playdough stick to the disk. Treat the playdough as a point mass. (a) If the disk is not rotating initially, what is its angular velocity after the collision? (b) What angular velocity would the disk need to have initially, if the disk stopped completely after the collision?

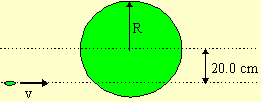
    (a) Since we have a collision in which there is a change in rotation, we apply the Law of Conservation of Momentum,

    Lf = Li .           (1)

    Initially the playdough is traveling in a straight line so its angular momentum is bmv, where b is the distance of closest approach to the point of rotation. Since everything will rotate about the centre of the disk, we take the centre as the point of rotation. Thus b = 0.20 m. After the collision, the playdough is stuck on the disk and rotates with the door in a circle. The angular momentum of an object moving in a circle is r2mΩ, where r is the radius of rotation. Clearly r = R, the radius of the disk.

    Initially the disk is not rotating and thus has no angular momentum. Afterwards, it is rotating and thus has an angular momentum given by IΩ. Consulting a table of moments of inertia, we find I = ½MR2.

    Thus equation (1) applied to this problem is

    R2mΩ + ½MR2Ω = bmv .

    Solving for Ω, we find

    Ω = bmv / [m + ½M]R2 = (0.2)(0.15)(5.5) / [(0.15) + ½(2.5)](0.35)2 = 0.962 rad/s .

    (b) If everything stops, Lf = 0. Equation (1) becomes

    0 = bmv + ½MR2Ω initial .

    Solving for Ωinitial, we get

    Ωinitial = 2bmv / MR2 = 2(0.2)(0.15)(5.5) / (2.5)(0.35)2 = -1.08 rad/s .

    The minus sign indicates that the disk would have to rotate clockwise.

    [Return to Top of Page]

  8. A 22-g bug crawls from the centre to the outside edge of a 150-g disk of radius 15.0 cm. The disk was rotating at 11.0 rad/s. What will be its final angular velocity? Treat the bug as a point mass.

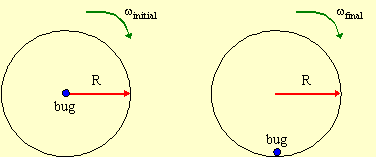
    There will be a change in rotation as the bug moves, so we use the Law of Conservation of Angular Momentum

    Lf = Li .           (1)

    Assuming that the bug doesn't slip then it rotates at the same velocity as the disk. Thus bug rotates in a circle. The angular momentum of an object moving in a circle is r2mΩ, where r is the radius of rotation. At the centre of the disk r = 0, initially. At the final position, the edge of the disk, r = R.

    The disk is rotating and thus has an angular momentum by IΩ. Consulting a table of moments of inertia, we find I = ½MR2.

    Thus equation (1) applied to this problem is

    R2mΩf + ½MR2Ωf = (0)2mΩi + ½MR2Ωi .

    Dividing through by ½R2 and solving for Ωf, we find

    Ωf = MΩi / (2m + M) = (0.15)(11.0 rad/s) / [2(0.022) + 0.150] = 8.51 rad/s .

    [Return to Top of Page]

  9. A cylindrical rod of radius r = 2.00 cm and mass 1.25 kg is upright on the edge of a rotating disk of mass 10.0 kg and radius 25.0 cm as is shown in diagram (a) below. The system is rotating at 15.0 rad/s. The rod falls on its side as shown in diagram (b). Diagrams (c) and (d) present a side view. What is the new angular velocity of the system? How much work was done in changing the shape of the object?

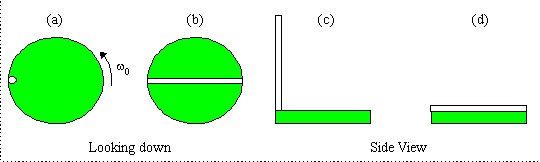
    As the system changes shape, there will be a change in rotation, so we use the Law of Conservation of Angular Momentum

    Lf = Li .           (1)

    Initially the cylindrical rod is a small disk rotating about the centre of the big disk The angular momentum of a rotating object is IΩ. However, note that the cylindrical rod is not rotating about its own centre of mass. We must use the parallel axis theorem with d = R - r. Consulting a table of moments of inertia, the moment for a small disk is Icm = ½mr2. When the cylindrical rod falls, it is still a rotating object and its angular momentum is given by IΩ, but now is has the shape of a rod. Consulting a table of moments of inertia, we find I =(1/12)mL2. According to the diagram, L = 2R = 0.50 m

    In both cases the disk is rotating and thus has an angular momentum by IΩ. Consulting a table of moments of inertia, we find I = ½MR2.

    Thus equation (1) applied to this problem is

    (1/12)mL2Ωf + ½MR2Ωf = [½mr2 + m(R-r)2]Ωi + ½MR2Ωi .

    Solving for Ωf, we find

    Ωf = {m[½r2 + (R-r)2] + ½MR2}Ωi / {(1/12)mL2 + ½MR2} .

    Substituting in the given values, we get

    [Return to Top of Page]

  10. A bicycle tire has a mass of 4.0 kg and a radius of 0.33 m. If it is rotating at 22 rad/s what is its angular momentum? If it is used as a gyroscope with a 24 cm long pivot bar, what will be its precession speed?

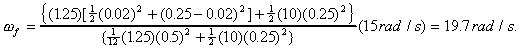
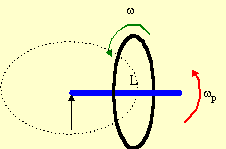
    The wheel is a rotating object so its angular momentum is given by IΩ. Treating the wheel as a hoop, I = mr2. Thus

    L = mr2Ω = (4 kg)(0.33 m)2(22 rad/s) = 9.583 kg-m2/s .

    The precession frequency is given by

    ωp = Rmg / L .

    The moment arm R is half the length of the bar L. Thus

    ωp = ½Lmg / L = ½(0.24 m)(4 kg)(9.81 m/s2) / (9.583 kg-m/s) = 0.162 rad/s .

    [Return to Top of Page]

[Return to Physics Homepage]     [Return to Mike Coombes' Homepage]     [Return to List of Handouts]     [Return to Problem Sets]     [Return to List of Solutions]

Questions? mike.coombes@kpu.ca

[Return to Kwantlen Homepage]