![[Return to Physics Homepage]](./../../physics.gif)
![[Return to Mike Coombes' Homepage]](./../../coombes.gif)
![[Return to List of Handouts]](./../../handouts.gif)
![[Return to Problem Sets]](./../../problems.gif)
![[Return to List of Solutions]](./../../solutions.gif)
| Questions: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
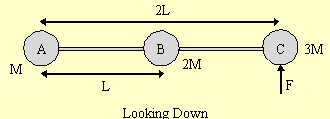
First we will calculate the moments of inertia. Since these are point masses we use the formula I = Σmi(ri)2:
(a) IA = M(0)2 + 2M(L)2 + 3M(2L)2 = 14ML2;
(b) Ib = M(L)2 + 2M(0)2 + 3M(L)2 = 4ML2.
The angular acceleration is governed by the rotational form of Newton's Second Law, Στz = Izαz, where z is out of the paper in this problem and τz, Iz, and αz are all determined relative to the same axis.
| Axis A | Axis B | |
| τz | 2LF | LF |
| Iz | 14ML2 | 4ML2 |
| Στz = Izαz | 2LF = 14ML2αA | LF = 4ML2αB |
So the acceleration about axis A is
and the acceleration about axis B is
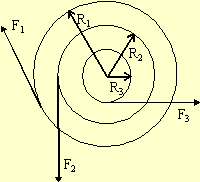
Since the axle is fixed we only need to consider the torques and
use Στz
= Izαz. Each of the
forces is tangential
to the object, i.e R and F are at 90º to one another. Recall that
clockwise torques are negative or into the paper in this case.
|
|
| -R1F1 + R2F2 + R3F3 = Iα |
So our equation for the acceleration is
Substituting in the given values, α = 1.88 rad/s2.

Since the problem wants accelerations and forces, and one object
rotates, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for each object. In
particular for any rotating body we must draw an extended FBD
in order to calculate the torques. Since the drum has a fixed
axle we need only consider the torques acting on it. Once the
diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz to get a
set of equations.
The forces acting directing on the block are weight and tension. Presumably the block will accelerate downwards. The only force directly acting on the drum which creates a torque is tension. Note that ropes, and therefore tensions, are always tangential to the object and thus normal to the radius. The other forces acting on the drum, the normal from the axle and the weight, both act through the CM and thus do not create torque. The drum accelerates counterclockwise as the block moves down.

| ΣFy = may | Στz = Izαz |
| T - Mg = -Ma | RT = Iα |
Since the rope is wrapped around the drum, we also have the relationship
a = Rα .
Referring to the table of Moments of Inertia, we find that I = ½mR2 for a solid cylinder. So our first equation is T = Mg - Ma. Our second is RT = ½mR2(a/R), or when we simplify T = ½ma. Putting this result into the first equation yields a = Mg / [M + ½m] = 1.353 m/s2. Thus α = a/R = 2.706 rad/s2. As well, T = ½ma = ½mMg / [M + ½m] = 84.56 N.

Since the problem wants accelerations and forces, and one object
rotates, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for each object. In
particular for any rotating body we must draw an extended FBD
in order to calculate the torques. Since the pulley has a fixed
axle we need only consider the torques acting on it. Once the
diagrams are drawn, we use ΣFx
= max, ΣFy =
may, and Στz
= Izαz to get a
set of equations.
The forces acting directing on the block on the table are weight,
a normal from the table, and tension. This block will accelerate
to the right. The forces acting directing on the hanging block
on the table are weight and tension. This block will accelerate
downwards. The only forces directly acting on the pulley which
creates torque are the tensions. Note that ropes, and therefore
tensions, are always tangential to the object and thus normal
to the radius. The tensions are different on either side of the
pulley because of static friction - which we don't need to consider.
The other forces acting on the pulley, the normal from the axle
and the weight, both act through the CM and thus do not create
torque. The pulley accelerates clockwise as the hanging block
moves down.

|
|
Pulley | Hanging Block | |
| ΣFx = max | ΣFy = may | Στz = Izαz | ΣFy = may |
| T1 = m1a | N - m1g = 0 | RT1 - RT2 = -Iα | T2 - m2g = -m2a |
From our table of Moments of Inertia, we find I = ½MR2 for a solid disk. As well, since the rope is strung over the pulley, we know a = Rα. Using these facts, the third equation becomes T1 - T2 = ½Ma. Using the first equation, T1 = m1a, and the second equation, T2 = m2g - m2a, we can eliminate T1 and T2 from the third equation:
Collecting terms that contain a, and rearranging yields,
The angular acceleration of the pulley is thus
The tension in the left side of the rope is given by
The tension in the hanging potion of the rope is
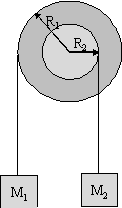
Since the problem wants accelerations and forces, and one object
rotates, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for each object. In
particular for any rotating body we must draw an extended FBD
in order to calculate the torques. Since the pulley has a fixed
axle we need only consider the torques acting on it. Once the
diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz to get a
set of equations.
The forces acting directing on the hanging blocks are weight and tension. Let's assume M1 accelerates downwards and thus M2 upwards. The only forces directly acting on the pulley which create torque are the tensions. Note that ropes, and therefore tensions, are always tangential to the object and thus normal to the radius. The tensions are different on either side of the pulley since they are different ropes. The other forces acting on the pulley, the normal from the axle and the weight, both act through the CM and thus do not create torque. The pulley accelerates counterclockwise as a result of our assumption for the acceleration of the blocks.
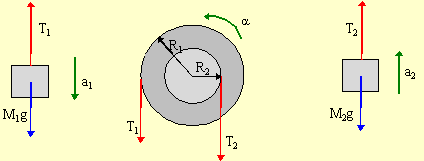
| Left | Pulley | Right |
| ΣFy = may | Στz = Izαz | ΣFy = may |
| T1 - M1g = -M1a1 | R1T1 - R2T2 = Iα | T2 - M2g = M2a2 |
(a) The acceleration of M1 is equal to the tangential acceleration of the outside of the winch, so a1 = αR1. The acceleration of M2 is equal to the tangential acceleration of the inside ring of the winch, so a2 = αR2.
(b) If we use the relationships from part (a), we can rewrite the equations in the table as
We use these results to eliminate T1 and T2
from the torque equation
Thus we find
(c) Using this results, and our previous equations for the tension in each string, we find
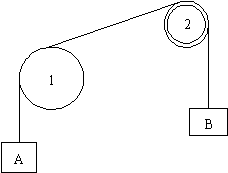
Since the problem wants accelerations and forces, and two objects
rotate, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for each object. In
particular for any rotating body we must draw an extended FBD
in order to calculate the torques. Since the pulleys have fixed
axles, we need only consider the torques acting on each. Once
the diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz
to get a set of equations.
The forces acting directing on the hanging blocks are weight and tension. Let's assume A accelerates downwards and thus B upwards. The only forces directly acting on the pulleys which create torque are the tensions. Note that ropes, and therefore tensions, are always tangential to the object and thus normal to the radius. The tensions are different on either side of the pulley due to static friction with the surface of the pulleys. The other forces acting on each pulley, the normal from the axle and the weight, both act through the CM and thus do not create torque. The blocks are connected by the same rope and thus have the same magnitude of acceleration. The rope does not slip as it goes over the pulleys, so the pulleys have the same tangential acceleration as the rope. Since the pulleys have different radii, they have different angular accelerations.
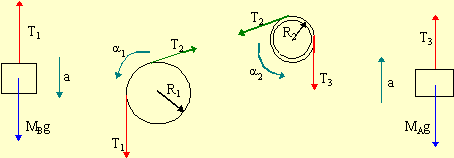
| Left | Disk Pulley | Hoop Pulley | Right |
| ΣFy = may | Στz = Izαz | Στz = Izαz | ΣFy = may |
| T1 - MAg = -MAa | RT1 - RT2 = Idiskα1 | R2T2 - R2T3 = Ihoopα2 | T3 - MBg = MBa |
In addition to the equations we have found above, we also know that the tangential acceleration of the pulleys is the same as the acceleration of the rope. Thus the angular acceleration of each pulley is related to a by α1 = a/R1 and α2 = a/R2. Examining a table of Moments of Inertia reveals that Idisk = ½Mdisk(R1)2 and Idisk = Mhoop(R2)2. Using this information allows us to rewrite the equations as
T1 - T2 = ½Mdiska (2),
T2 - T3 = Mhoopa (3), and
T3 =MBg + MBa (4).
If we add equations (2) and (3) together, we get
Then equations (1) and (4) can be used to eliminate T1
and T3 from the above
Collecting terms involving a and rearranging yields,
Using the above result, we find the angular accelerations
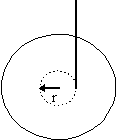
Since the problem wants an acceleration, and an object rotates,
that suggests we must use both the linear and rotational versions
of Newton's Second Law. Applying Newton's Second Law requires
that we draw free body diagrams for each object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the yo-yo does not have a fixed
axle, we need consider the torques acting about the CM. Once
the diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz
to get a set of equations.
The forces acting directing on the hanging yo-yo are weight and
tension. Let's assume it accelerates downwards. The only force
directly acting on the pulley which creates a torque is the tensions,
the weight acts from the CM and cannot create a torque. Note
that strings, and therefore tensions, are always tangential to
the object and thus normal to the radius.
The yo-yo is said to roll without slipping. That phrase means
that the angular acceleration of the yo-yo about its CM is related
to its linear acceleration by a = Rα.
Note that since the string is tied around the inner cylinder; it is that radius which figures
into the relation.

| ΣFy = may | Στz = Izαz |
| T - mg = -ma | rT = Iαcm |
Since αcm = a/r, we have two
simple equations
Eliminating T from the first equation yields,
Since the problem wants an acceleration, and an object rotates,
that suggests we must use both the linear and rotational versions
of Newton's Second Law. Applying Newton's Second Law requires
that we draw free body diagrams for the object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the ball does not have a fixed
axle, we need consider the torques acting about the CM. Once
the diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz
to get a set of equations.
The forces acting directly on the ball are the normal, weight, and friction. Naturally the cylinder will accelerate downward the incline. Since the cylinder isn't slipping, its forward rate of rotation, its angular acceleration, is also forward. The only force directly acting on the cylinder which creates a torque is the friction, the normal and the weight act through the CM and cannot create a torque. Note that friction, being along the surface, is tangential to the cylinder and thus normal to the radius.
The cylinder is said to roll without slipping. That phrase means that the angular acceleration of the ball about its CM is related to its linear acceleration by a = Rα.
The type of friction is static since we are told that the cylinder
is rolling without slipping. The only point left to resolve is
in which direction it points. Since friction creates the only
torque, and we have decided that α is forward, then friction must
be up the incline. Only point to be careful about is that in
rolling problems, one seldom is dealing with the fs
MAX unless it is explicitly stated.
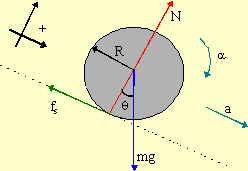
| ΣFx = max | ΣFy = may | Στz = Izαz |
| mgsinθ - fs = ma | N - mgcosθ = 0 | -Rfs = -Icylαcm |
(a) The first equation is mgsinθ - ma = fs. The third equation can be simplified by using the given value for Icyl and by noting that αcm = a/R. Then the third equation becomes
This can be substituted into the first equation to get
Solving for a yields
(b) We can use this result with fs = ½ma, to get an expression for fs,
However, the maximum value of fs is μsN.
The second equation gives N = mgcosθ, so
Using (1) and (2) to eliminate fs, yields
Using the identity tanθ
= sinθ/cosθ,
we get
This is the angle at which the cylinder would start to slip as
it moved down the incline.
Since the problem wants an acceleration, and an object rotates,
that suggests we must use both the linear and rotational versions
of Newton's Second Law. Applying Newton's Second Law requires
that we draw free body diagrams for the object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the hoop does not have a fixed
axle, we need to consider the torques acting about the CM. Once
the diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz
to get a set of equations.
The forces acting directing on the hoop are the normal, weight,
and friction. As the hoop goes up the incline it is slowing down,
so its acceleration is down the incline. Since the hoop isn't
slipping, its forward rate of rotation, its angular acceleration,
is decreasing. The only force directly acting on the hoop which
creates a torque is the friction, the normal and the weight act
through the CM and cannot create a torque. Note that friction,
being along the surface, is tangential to the hoop and thus normal
to the radius.
The hoop is said to roll without slipping. That phrase means
that the angular acceleration of the hoop about its CM is related
to its linear acceleration by a = Rα.
The type of friction is static since we are told that the hoop is rolling without slipping. The only point left to resolve is in which direction it points. Since friction creates the only torque, and we have decided that α is backward, then friction must be up the incline. One point to be careful about is that in rolling problems, one seldom is dealing with the fs MAX unless it is explicitly stated.
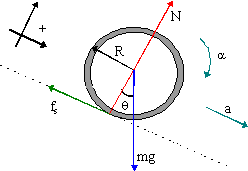
| ΣFx = max | ΣFy = may | Στz = Izαz |
| mgsinθ - fs = ma | N - mgcosθ = 0 | -Rfs = -Ihoopαcm |
(a) The first equation is mgsinθ - ma = fs. The third equation can be simplified by using the given value for Ihoop and by noting that αcm = a/R. Then the third equation becomes
This can be substituted into the first equation to get
Solving for a yields
(b) We can use this result with fs = ma, to get an expression for fs,
However, the maximum value of fs is μsN. The second equation gives N = mgcosθ, so
Using (1) and (2) to eliminate fs, yields
Using the identity tanθ
= sinθ/cosθ, we get
This is the angle at which the hoop would start to
slip as it moved down the incline.

Since the problem wants an acceleration, and objects
rotate, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for the object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the wheel axle is not fixed, we
need consider the torques acting about each wheel's CM. Once
the diagrams are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz
to get a set of equations.
The forces acting directly on each wheel are the normal, weight, and friction. Naturally the car will accelerate downward the incline. We will assume that each wheel supports one quarter of the car's weight and thus are all identical - we need only one FBD. Since the wheel isn't slipping, its forward rate of rotation, its angular acceleration, is also forward. The only force directly acting on the wheel which creates a torque is the friction, the normal and the weight act through the CM and cannot create a torque. Note that friction, being along the surface, is tangential to the wheel and thus normal to the radius.
The wheel is said to roll without slipping. That phrase means that
the angular acceleration of the wheel about its CM is related to its
linear acceleration by a = Rα.
The type of friction is static since we are told
that the wheel is rolling without slipping. The only point left
to resolve is in which direction it points. Since friction creates
the only torque, and we have decided that α
is forward, then friction must be up the incline. One point to be careful
about is that in rolling problems, one seldom is dealing with the
fs MAX unless it is explicitly stated.
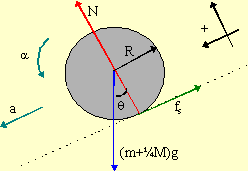
| ΣFx = max | ΣFy = may | Στz = Izαz |
| (m+¼M)gsinθ - fs = (m+¼M)a | N - (m+¼M)gcosθ = 0 | Rfs = Idiskαcm |
(a) The first equation is mgsinθ - ma = fs. The third equation can be simplified by using Ihoop = ½mR2 and by noting that αcm = a/R. Then the third equation becomes
This can be substituted into the first equation to get
Solving for a yields
(b) We can use this result with fs = ½ma, to get an expression for fs,
However, the maximum value of fs is
μsN. The second equation gives N
= (m+¼M)gcosθ, so
Using (1) and (2) to eliminate fs, yields
Using the identity tanθ
= sinθ/cosθ, we get
This is the angle at which the wheels would start to slip as it moved down the incline.
We apply Newton's Second Law to the problem.
|
Σ Fx |
= max |
Σ Fy |
= may |
Σ τcm |
= Icmα cm |
|
− Fcos(θ ) + fs |
= − Ma |
N + Fsin(θ ) − Mg |
= 0 |
Rfs |
= Iα |
We also know that a = Rα and I = ½MR2. We substitute these relationships into the torque equation
|
Rfs = ½MR2(a/R) |
(1) |
This yields an equation for fs,
|
fs = ½Ma |
(2) |
We take this result and substitute it into the x-component equation
|
− Fcos(θ ) + ½Ma = − Ma |
(3) |
Solving for a, as required in part (a), yields
|
a = (2/3)(F/M) cos(θ ) |
(4) |
We can also find fs, as required in part (b), by substituting (4) back into Eqn. (2);
|
fs = (1/3)Fcos(θ ) |
(5) |
|
fsmax = μs[Mg − Fsin(θ )] |
(6) |
Equating Eqns. (5) and (6) will tell us the value of F at which slipping occurs
|
(1/3)Fcos(θ )= μs[Mg − Fsin(θ )] |
(7) |
We get F by itself on the left-hand side
|
F[(1/3)cos(θ ) + μssin(θ )] = μsMg |
(8) |
|
|
(9) |
We know there is a normal and weight acting on the yo-yo but these do not create torques as they operate on or through the Centre of Mass. There is non-maximum static friction acting but we must determine it's direction. First if there were no T, there would be no friction. T is twisting the yo-yo counterclockwise pushing the yo-yo into the surface. The surface reacts by pushing back. The FBD looks like
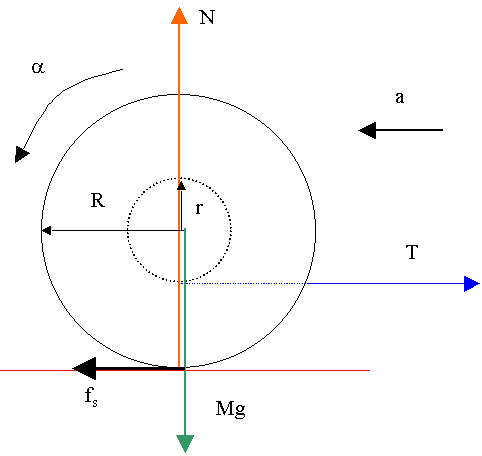
Here I have guessed that the yo-yo will roll backwards. Notice that my choice of a and α are consistent.
I apply Newton's Second Law
|
Σ Fx |
= max |
Σ Fy |
= may |
Σ τcm |
= Icmacm |
|
T − fs |
= − Ma |
N − Mg |
= 0 |
rT − Rfs |
= Iα |
We also know a = Rα .
The torque equation becomes can be solved for fs
|
fs = (r/R)T − (I/R2)a . |
(1) |
We substitute this into the x-component equation
|
T − [(r/R)T − (I/R2)a] = − Ma |
(2) |
We bring the term involving a from the left to the right and solve for a in terms of T,
|
T(R-r)/R = − (M + I/R2)a |
(3) |
or
|
|
(4) |
The fact that a is negative tells me that my guess about the direction of a and α are wrong. The acceleration is forward and counterclockwise.
Substituting Eqn. (4) into Eqn. (1), we find
|
|
(5) |
Since fs is positive, it must be have been chosen in the right direction.
Now as we see from Eqn. (5), as T increases so does fs. We know fs £ μsN or fs £ μsMg in our case when we make use of the y-component equation. Thus we have a limit on T
|
|
(6) |
This yields the result
|
|
(7) |
If T is any bigger, the yo-yo will slip.

Since the problem involves forces, and an object
rotates, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for the object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the bowling ball does not have
a fixed axle, we need to consider the torques acting about the
CM. Once the diagrams are drawn, we use
ΣFx = max,
ΣFy = may,
and Στz
= Izαz
to get a set of equations.
The forces acting directing on the bowling ball
are the normal, weight, and friction. The only force directly
acting on the bowling ball which creates a torque is the friction,
the normal and the weight act through the CM and cannot create
a torque. Note that friction, being along the surface, is tangential
to the bowling ball and thus normal to the radius.
The bowling ball is said to be slipping. That phrase means that the angular acceleration of the bowling ball about its CM is NOT related to its linear acceleration, i.e. by a ≠ rα. It also means that we are dealing with kinetic friction. The only point left to resolve is in which direction it points. To do this examine the tangential velocity of the outside rim of the bowling ball, v = Rω0 = 3v0. This means the rim is spinning much faster than the CM is moving forward; friction will act to slow the rim as the rim rubs on the surface of the bowling lane. Friction will point in the direction of the initial velocity. Since friction causes the only torque, the angular acceleration is backwards.

| ΣFx = max | ΣFy = may | Στz = Izαz |
| fk = ma | N - mg = 0 | Rfk = Icmα |
We also know that fk = μN. Since
the second equation gives N = mg, we have fk
= μmg. The first equation thus yields
A bowling ball is a solid sphere and using a table of moments
of inertia we find I = (2/5)mR2. With our expression
for fk, our third equation becomes
or on rearranging,
Time is a kinematics variable. We have initial velocities and
accelerations so we can write expressions for the linear and rotational
velocity as a function of time
and
Note that a increases the linear velocity but α decreases the angular velocity. This explains the + in (3) and the − in (4).
We want the time when
Substituting in equation (3) and (4), we get
Solving for t yields
This is the time that is takes for the bowling ball to start to
roll without slipping. Plugging this result back into equation
(3) gives us the linear velocity of the bowling ball at this and
all later times
Making use of another kinematics formula, we find the distance
traveled,
![[Return to Top of Page]](./../../top.gif)
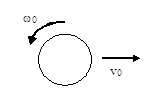
Since the problem involves forces, and an object
rotates, that suggests we must use both the linear and rotational
versions of Newton's Second Law. Applying Newton's Second Law
requires that we draw free body diagrams for the object. In particular
for any rotating body we must draw an extended FBD in order to
calculate the torques. Since the bowling ball does not have
a fixed axle, we need to consider the torques acting about the
CM. Once the diagrams are drawn, we use
ΣFx = max,
ΣFy = may,
and Στz
= Izαz
to get a set of equations.
The forces acting directing on the bowling ball
are the normal, weight, and friction. The only force directly
acting on the bowling ball which creates a torque is the friction,
the normal and the weight act through the CM and cannot create
a torque. Note that friction, being along the surface, is tangential
to the bowling ball and thus normal to the radius.
The bowling ball is said to be slipping. That phrase means that the angular acceleration of the bowling ball about its CM is NOT related to its linear acceleration, i.e. by a ≠ rα. It also means that we are dealing with kinetic friction. The only point left to resolve is in which direction it points. To do this examine the tangential velocity of the outside rim of the bowling ball, v = Rω0 = v0. The tangential velocity and the centre of mass velocity are in the same direction. Friction will act to reverse the spin as the rim rubs on the surface of the bowling lane. Friction will point in the direction of the initial velocity. Since friction causes the only torque, the angular acceleration is backwards.
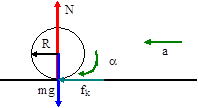
| ΣFx = max | ΣFy = may | Στz = Izαz |
| fk = ma | N - mg = 0 | Rfk = Icmα |
We also know that fk = μN. Since
the second equation gives N = mg, we have fk
= μmg. The first equation thus yields
A bowling ball is a solid sphere and using a table of moments
of inertia we find I = (2/5)mR2. With our expression
for fk, our third equation becomes
or on rearranging,
Time is a kinematics variable. We have initial velocities and
accelerations so we can write expressions for the linear and rotational
velocity as a function of time
and
Note that a decreases the linear velocity but α increases the
clockwise angular velocity. This explains the − in (3) and the + in (4).
We want the time when
Substituting in equation (3) and (4), we get
Solving for t yields
This is the time that is takes for the bowling ball to start to
roll without slipping. Plugging this result back into equation
(3) gives us the linear velocity of the bowling ball at this and
all later times
Making use of another kinematics formula, we find the distance
traveled,
![[Return to Top of Page]](./../../top.gif)

Since the problem involves forces, and an object rotates, that
suggests we must use both the linear and rotational versions of
Newton's Second Law. Applying Newton's Second Law requires that
we draw free body diagrams for the object. In particular for
any rotating body we must draw an extended FBD in order to calculate
the torques. Since the ball does not have a fixed axle, we need
to consider the torques acting about the CM. Once the diagrams
are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz to get a
set of equations.
The forces acting directing on the ball are the normal, weight,
and friction. The only force directly acting on the ball which
creates a torque is the friction, the normal and the weight act
through the CM and cannot create a torque. Note that friction,
being along the surface, is tangential to the ball and thus normal
to the radius.
The ball is said to be slipping. That phrase means that the angular
acceleration of the bowling ball about its CM is NOT related to
its linear acceleration, i.e. by a ≠ rα.
It also means that we are dealing with kinetic friction. The only point
left to resolve is in which direction it points. To do this examine the
tangential velocity of the outside rim of the bowling ball, v = 0 since it
wasn't rotating. This means the rim will rub on the rough surface as
it moves to the right and thus it will experience kinetic friction
to the left opposite to the direction of the initial velocity.
Since friction causes the only torque, the angular acceleration
is forward.
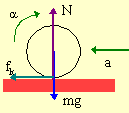
| ΣFx = max | ΣFy = may | Στz = Izαz |
| -fk = -ma | N - mg = 0 | -Rfk = -Iαcm |
We also know that fk = μN. Since the second equation gives N = mg, we have fk = μmg. The first equation thus yields
Consulting a table of moments of inertia, we find I = (2/5)mR2
for solid sphere. With our expression for fk, our
third equation becomes
or, on rearranging,
Our results indicate that the forward motion slows as the forward
rotation increases.
Time is a kinematics variable. We have initial velocities and
accelerations so we can write expressions for the linear and rotational
velocity as a function of time
and
We want the time when |v(t)| = |Rω(t)|, where
the absolute bars are there to stress that we are relating magnitudes
and must be careful with signs.
Substituting in equation (3) and (4), we get
Solving for t yields
This is the time that is takes for the bowling ball to start to
roll without slipping. Plugging this result back into equation
(3) gives us the linear velocity of the bowling ball at this and
all later times
Making use of another kinematics formula, we find the distance
traveled,

Since the problem involves forces, and an object rotates, that
suggests we must use both the linear and rotational versions of
Newton's Second Law. Applying Newton's Second Law requires that
we draw free body diagrams for the object. In particular for
any rotating body we must draw an extended FBD in order to calculate
the torques. Since the ball does not have a fixed axle, we need
to consider the torques acting about the CM. Once the diagrams
are drawn, we use ΣFx
= max, ΣFy
= may, and Στz
= Izαz to get a
set of equations.
The forces acting directing on the ball at point A are the normal,
weight, and friction. The only force directly acting on the ball
which creates a torque is the friction, the normal and the weight
act through the CM and cannot create a torque. Note that friction,
being along the surface, is tangential to the ball and thus normal
to the radius.
The ball starts to slip at A. That phrase means that the angular acceleration of the bowling ball about its CM is NOT related to its linear acceleration, i.e. by a a ≠ rα. It also means that we are dealing with kinetic friction. The only point left to resolve is in which direction it points. To do this examine the tangential velocity of the outside rim of the bowling ball; v = 0 since it wasn't rotating. This means the rim will rub on the rough surface as it moves down the incline and thus it will experience kinetic friction up the incline opposite to the direction of the velocity. Since friction causes the only torque, the angular acceleration is counterclockwise.

| ΣFx = max | ΣFy = may | Στz = Izαz |
| -fk + mgsinθ = ma | N - mgcosθ = 0 | Rfk = Iαcm |
We also know that fk = μN. Since the
second equation gives N = mgcosθ, we have fk
= μmgcosθ. The first
equation thus yields
Consulting a table of moments of inertia, we find I = (2/3)mR2
for a hollow sphere. With our expression for fk, our
third equation becomes
or, on rearranging,
Our results indicate that the linear motion is slower than with no friction and that the counterclockwise rotation increases.
Time is a kinematics variable. We have initial velocities and
accelerations so we can write expressions for the linear and rotational
velocity as a function of time
and
We want the time when v(t) = Rω(t), where the
absolute bars are there to stress that we are relating magnitudes and must
be careful with signs.
Substituting in equation (3) and (4), we get
Collecting the terms involving t together
or, more simply
Solving for t yields
This is the time that is takes for the bowling ball to start to
roll without slipping. Notice that the denominator could be zero
or even negative for some angles - that is at those angles the
ball never stops slipping. Plugging the given values into this
result, we get t = 3.5886 seconds.
Putting this result back into equation (3) gives us the linear
velocity of the bowling ball at this and all later times
With the given values this becomes vf = 9.9243 m/s.
Making use of another kinematics formula, we find the distance traveled,
or, after rearranging,
The numeric value of which is x = 25.88 m .
Questions? mike.coombes@kpu.ca